Problem #PRU-65309
Problems
Probability and statistics
Probability theory
Continuous distribution
Algebra
Mean values
Methods
Algebraic methods
Proof by exhaustion
Problem
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.
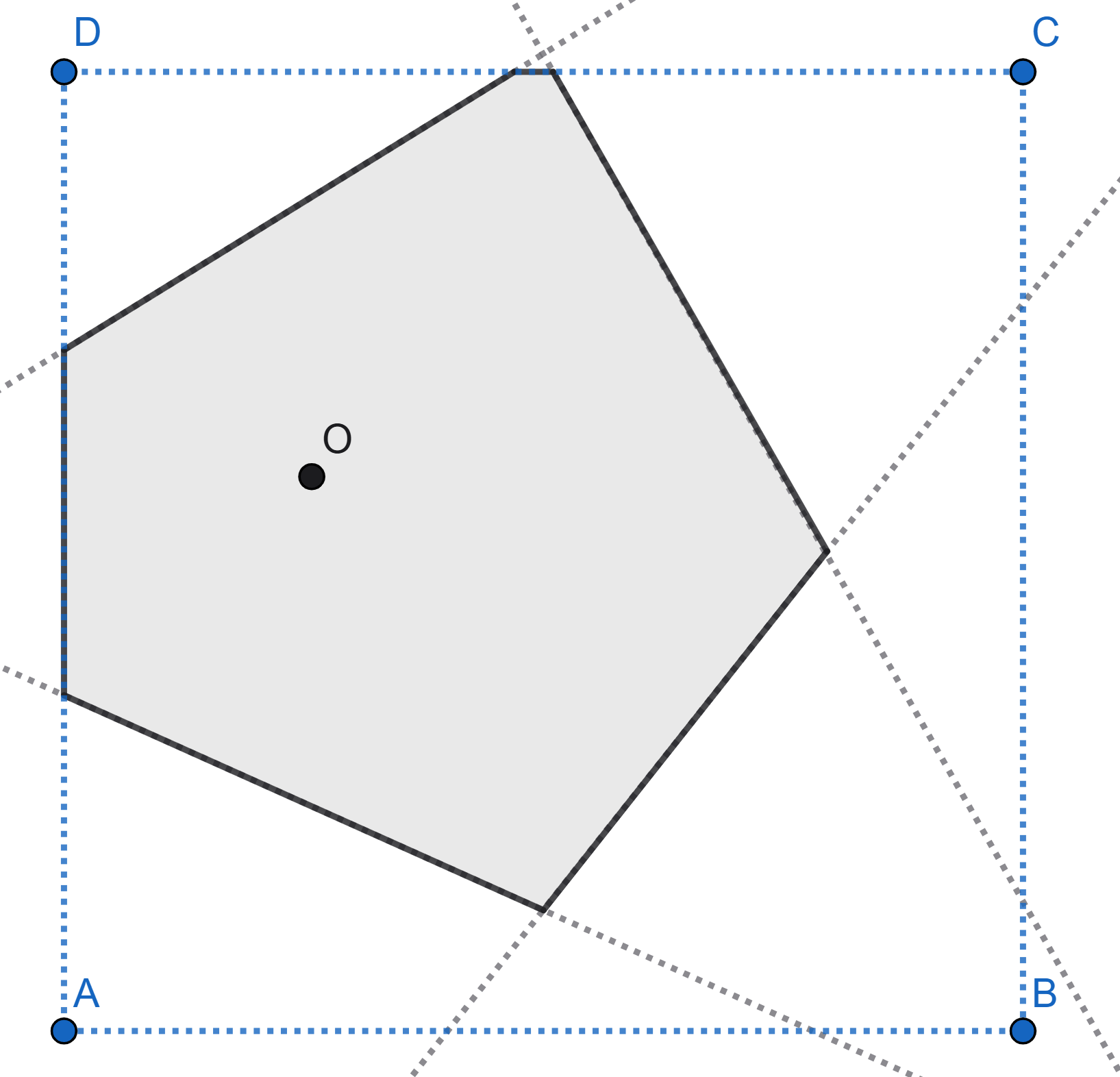
To see the solution register and get verified.