Problem #PRU-67173

Problem

In the middle of an empty pool there is a square platform of \(50 \times 50\) cm, split into cells of \(10\times 10\) cm. Sunny builds towers of \(10\times 10\times 10\)cm cubes on the platform cells. After that his friend Margo turns on the water and counts how many towers are still above the water level. They call each visible tower an island.

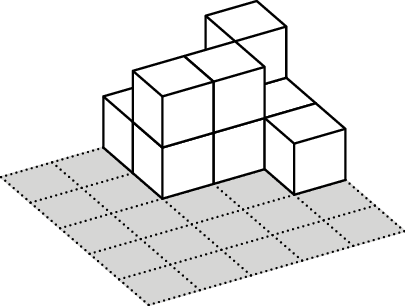
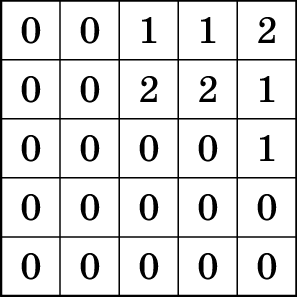
For example, let’s consider the case when the heights of the towers are as given in the table on the right. Then at the water level of \(5\) cm there is \(1\) island, at the water level of \(15\) cm there are two islands (if the islands have a common corner or don’t intersect at all, they are considered separate islands), and at the water level of \(25\) cm, all the towers are covered with water and there are \(0\) islands.

Find out how Sunny should build his towers to get the following numbers of islands corresponding to the level of water in the pool: \[\begin{array}{@{}*{26}{c}@{}} \textit{Water level (cm)}& 5& 15& 25& 35& 45\\ \textit{Number of islands}& 2& 5& 2& 5& 0 \end{array}\]

In the solution, write down how many cubes are there composing a tower in each cell as it is done in the example.