Problem #DES-141023
Problem
Today we will focus on the study of Euclidean geometry of plane figures. Around 300 BCE a Greek mathematician Euclid developed a rigorous way to study plane geometry in his work Elements based on axioms (statement assumed to be correct) and theorems (statements deduced from axioms). The axioms of Euclidean Elements are the following:
For any two different points, there exists a line containing these two points, and this line is unique.
A straight line segment can be prolonged indefinitely.
A circle is defined by a point for its centre and a distance for its radius.
All right angles are equal.
For any line \(L\) and point \(P\) not on \(L\), there exists a line through \(P\) not meeting \(L\), and this line is unique.
In examples we deduce from the axioms above the following basic
principles:
1. The supplementary angles (angles "hugging" a straight line) add up to
\(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
3. A line cutting two parallel lines cuts them at the same angles (these
are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), the
two angles touching the third side are equal.
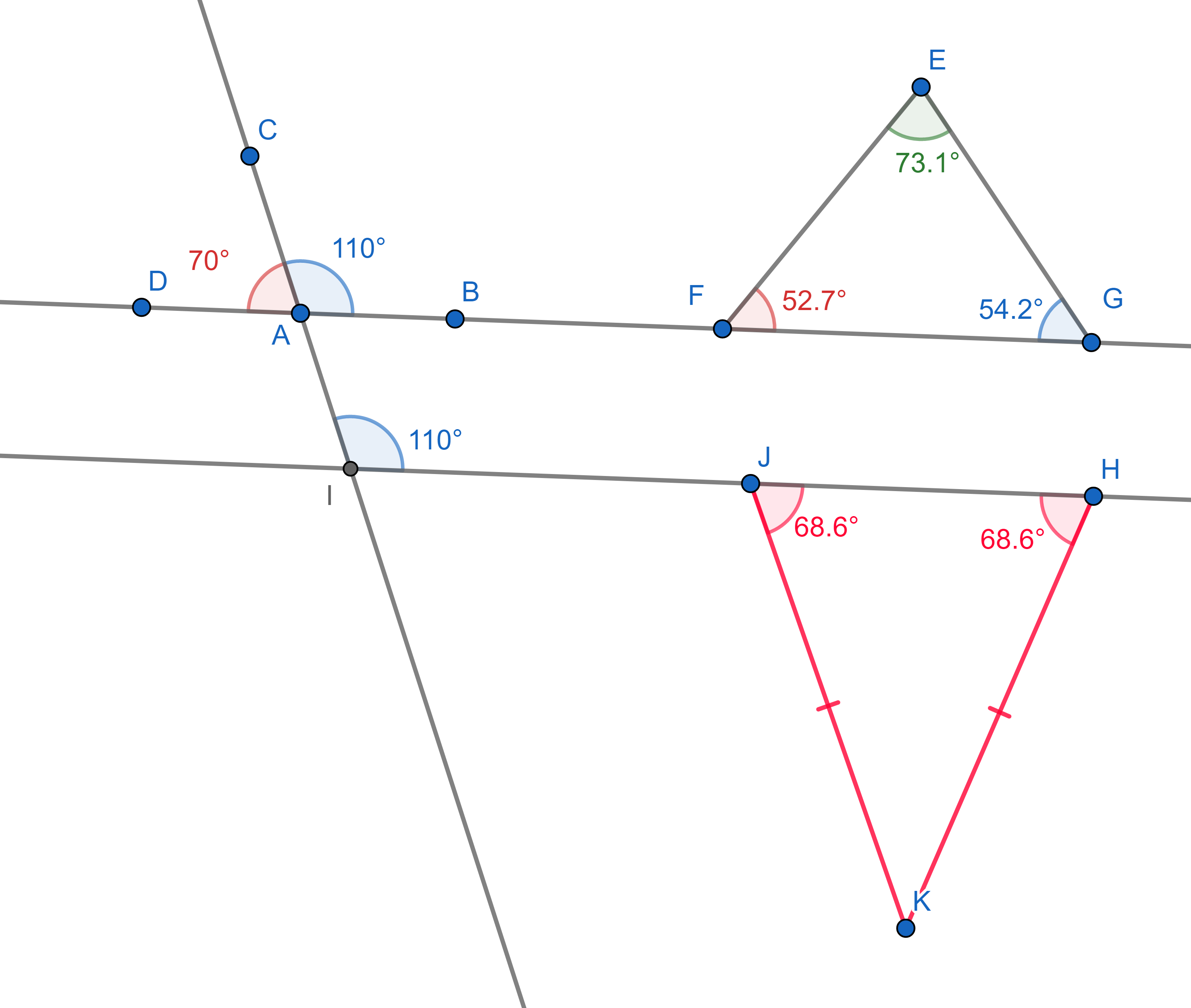
Let’s have a look at some examples of how to apply these axioms to prove geometric statements.