Problem #PRU-5086

Problems Geometry
 10–15  3.0

Problem

Consider the following "proof" that any triangle is equilateral: Given a triangle \(ABC\), we first prove that \(AB = AC\). First let’s draw the bisector of the angle \(\angle A\). Now draw the perpendicular bisector of segment \(BC\), denote by \(D\) the middle of \(BC\) and by \(O\) the intersection of these lines. See the diagram
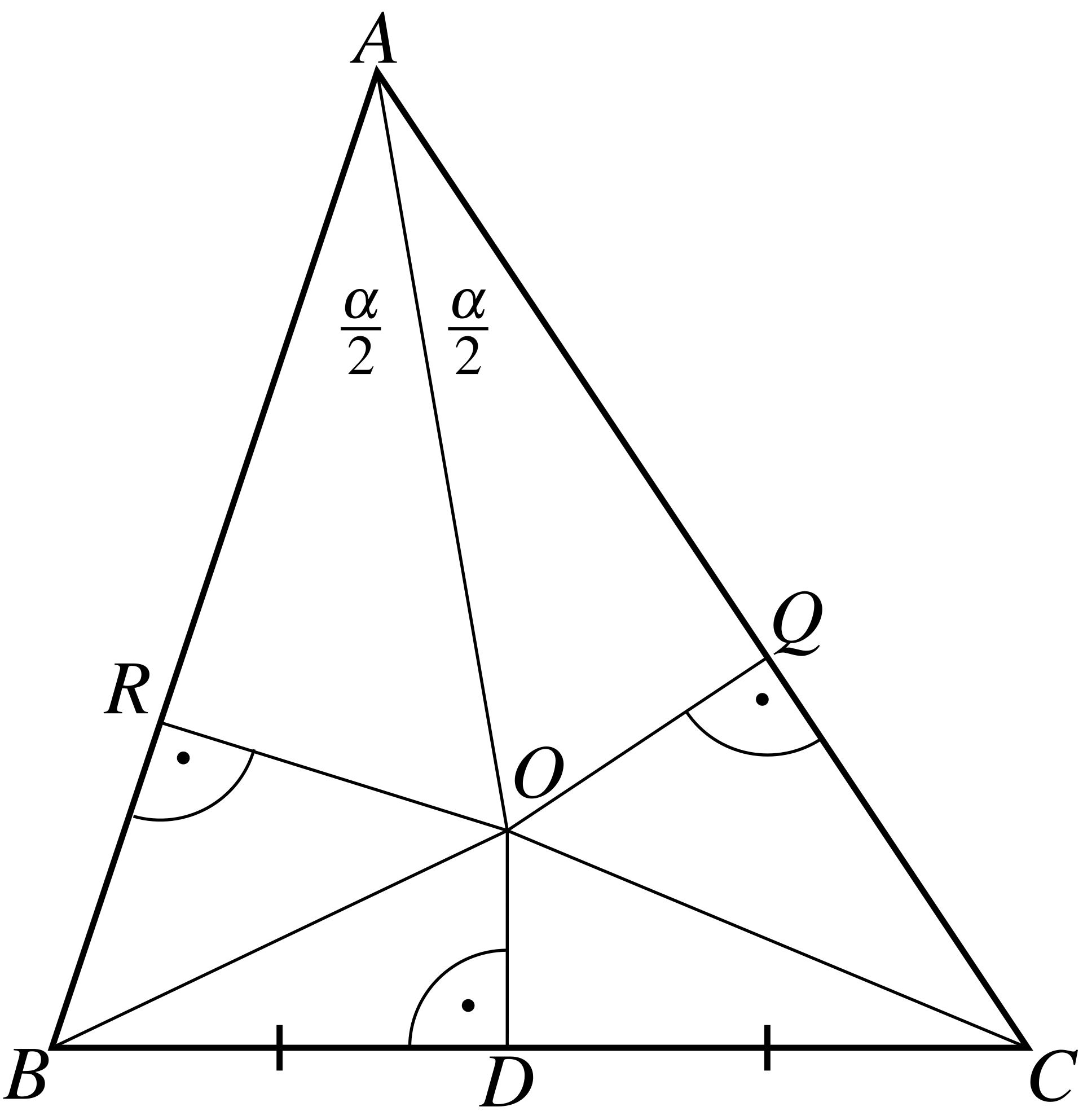
image
Draw the lines \(OR\) perpendicular to \(AB\) and \(OQ\) perpendicular to \(AC\). Draw lines \(OB\) and \(OC\). Then the triangles, \(RAO\) and \(QAO\) are equal, since we have equal angles \(\angle ORA = \angle OQA = 90°,\) and \(\angle RAO = \angle QAO,\) and the common side \(AO\). On the other hand the triangles \(ROB\) and \(QOC\) are also equal since the angles \(\angle BRO = \angle CQO = 90°\), the hypotenuses \(BO = OC\) the legs \(RO = OQ\). Thus, \(AR = AQ,\) \(RB = QC,\) and \(AB = AR + RB = AQ + QC = AC.\) Q.E.D.

As a corollary, one can show that all the triangles are equilateral, by showing that \(AB = BC\) in the same way.