Problem #PRU-5089
Problem
Let’s prove that any \(90^{\circ}\)
angle is equal to any angle larger than \(90^{\circ}\). On the diagram
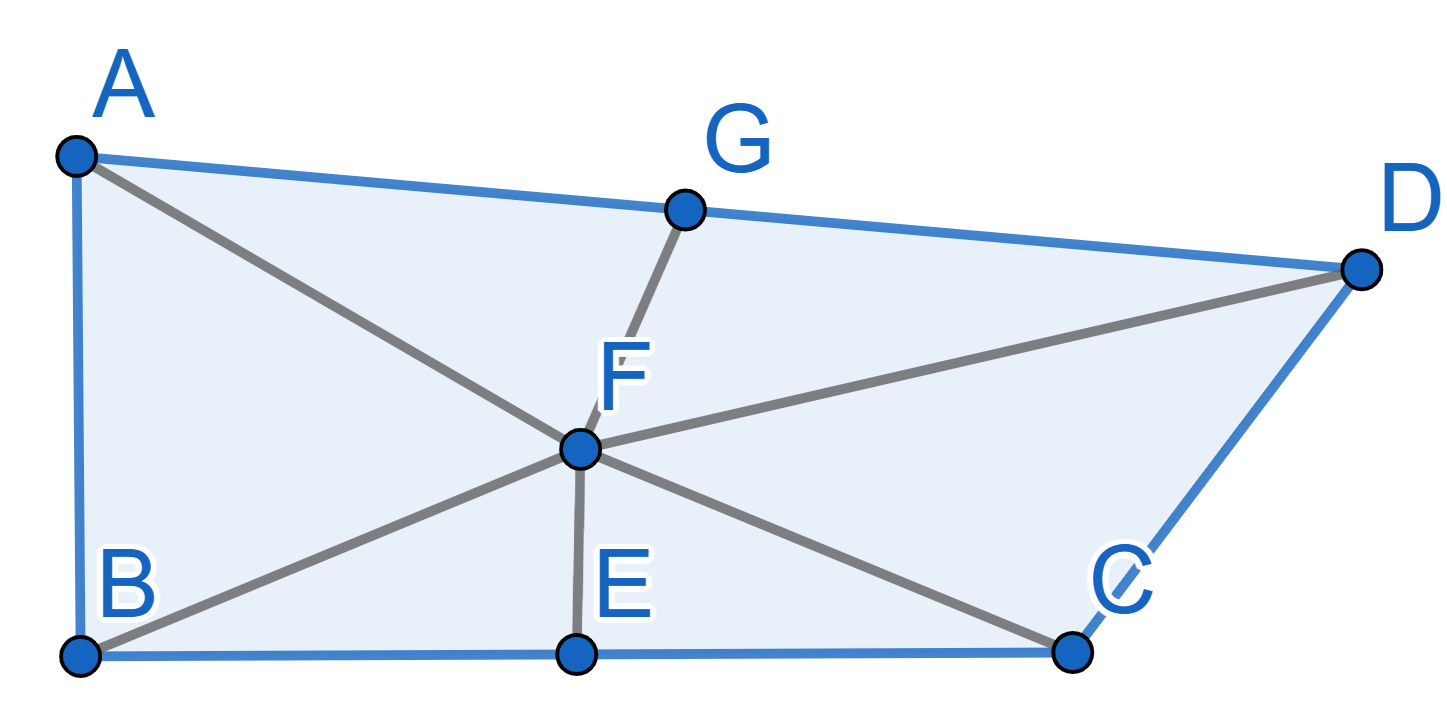
We have the angle \(\angle ABC =
90^{\circ}\) and angle \(\angle BCD>
90^{\circ}\). We can choose a point \(D\) in such a way that the segments \(AB\) and \(CD\) are equal. Now find middles \(E\) and \(G\) of the segments \(BC\) and \(AD\) respectively and draw lines \(EF\) and \(FG\) perpendicular to \(BC\) and \(AD\).
Since \(EF\) is the middle
perpendicular to \(BC\) the triangles
\(BEF\) and \(CEF\) are equal which implies the equality
of segments \(BF\) and \(CF\) and of angles \(\angle EBF = \angle ECF\), the same about
the segments \(AF=FD\). By condition we
have \(AB=CD\), thus the triangles
\(ABF\) and \(CDF\) are equal, thus \(\angle ABF = \angle DCF\). But then we have
\[\angle ABE = \angle ABF + \angle FBE =
\angle DCF + \angle FCE = \angle DCE.\]