Problem #PRU-5120

Problem

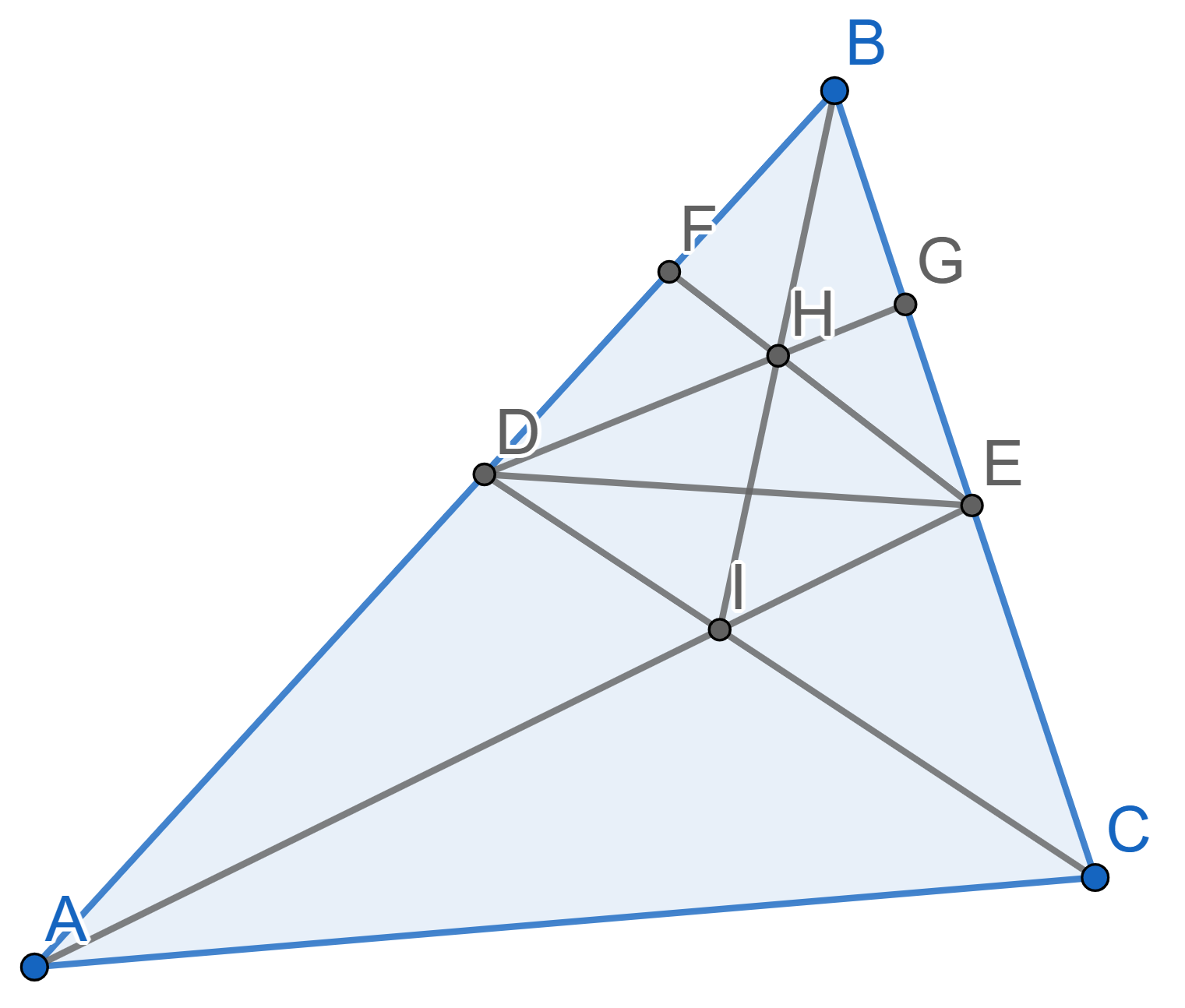
In the triangle \(ABC\) the lines \(AE\) and \(CD\) are the bisectors of the angles \(\angle BAC\) and \(\angle BCA\), intersecting at the point \(I\). In the triangle \(BDE\) the lines \(DG\) and \(EF\) are the bisectors of the angles \(\angle BDE\) and \(\angle BED\), intersecting at the point \(H\). Prove that the points \(B,\,H,\, I\) are situated on one straight line.