Problem #DES-020324
Problem
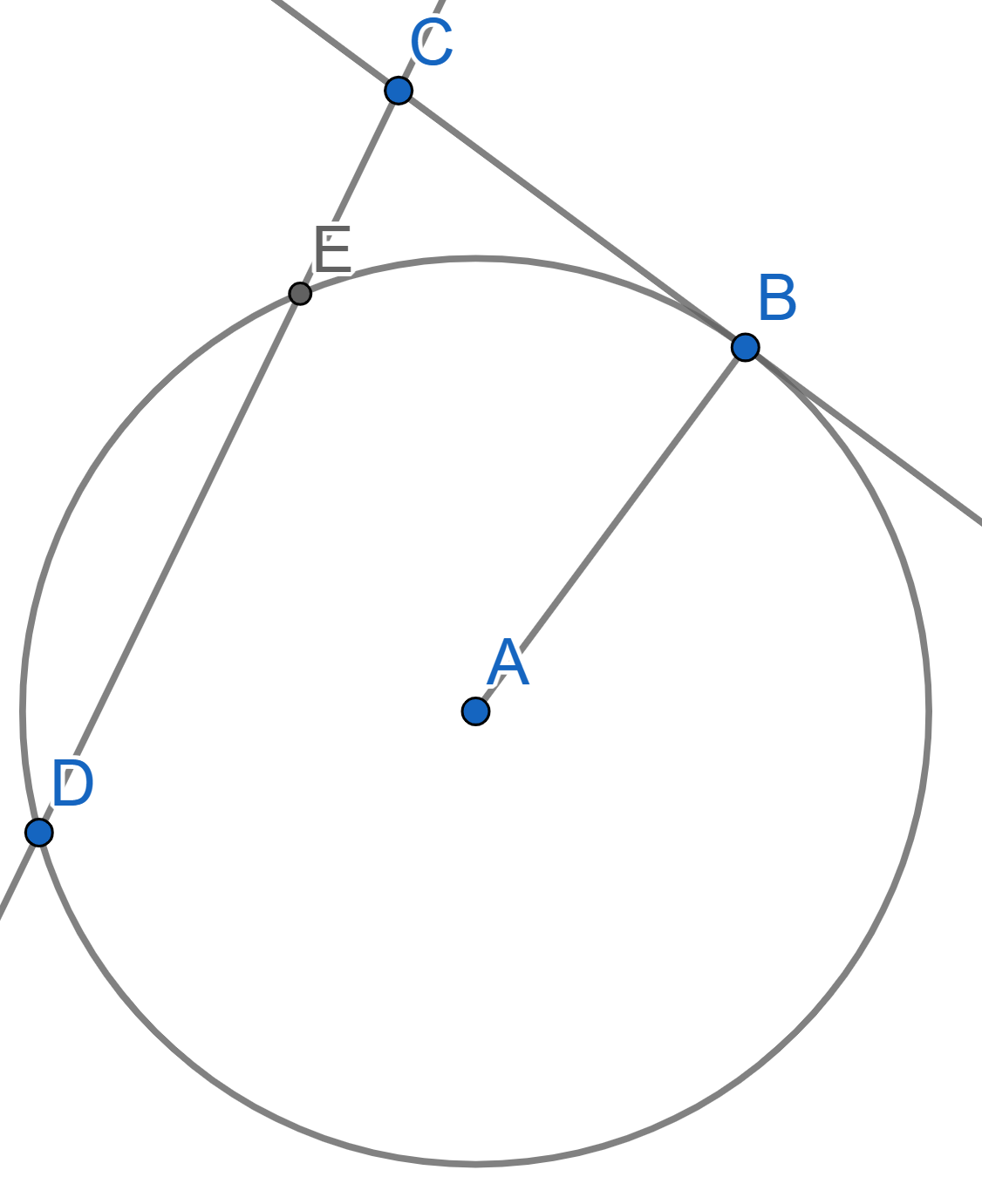
Generally, when a line intersects a circle, it creates two different
points of intersection. However, sometimes there is only one point. In
such case we say the line is tangent to the circle. For
example on the picture below the line \(CD\) intersects the circle at two points
\(D\) and \(E\) and the line \(CB\) is tangent to the circle. To solve the
problems today we will need the following theorem.
Theorem: The radius \(AB\) is perpendicular to the tangent line
\(BC\).
To see the solution register and get verified.