Problem #PRU-5207

Problem

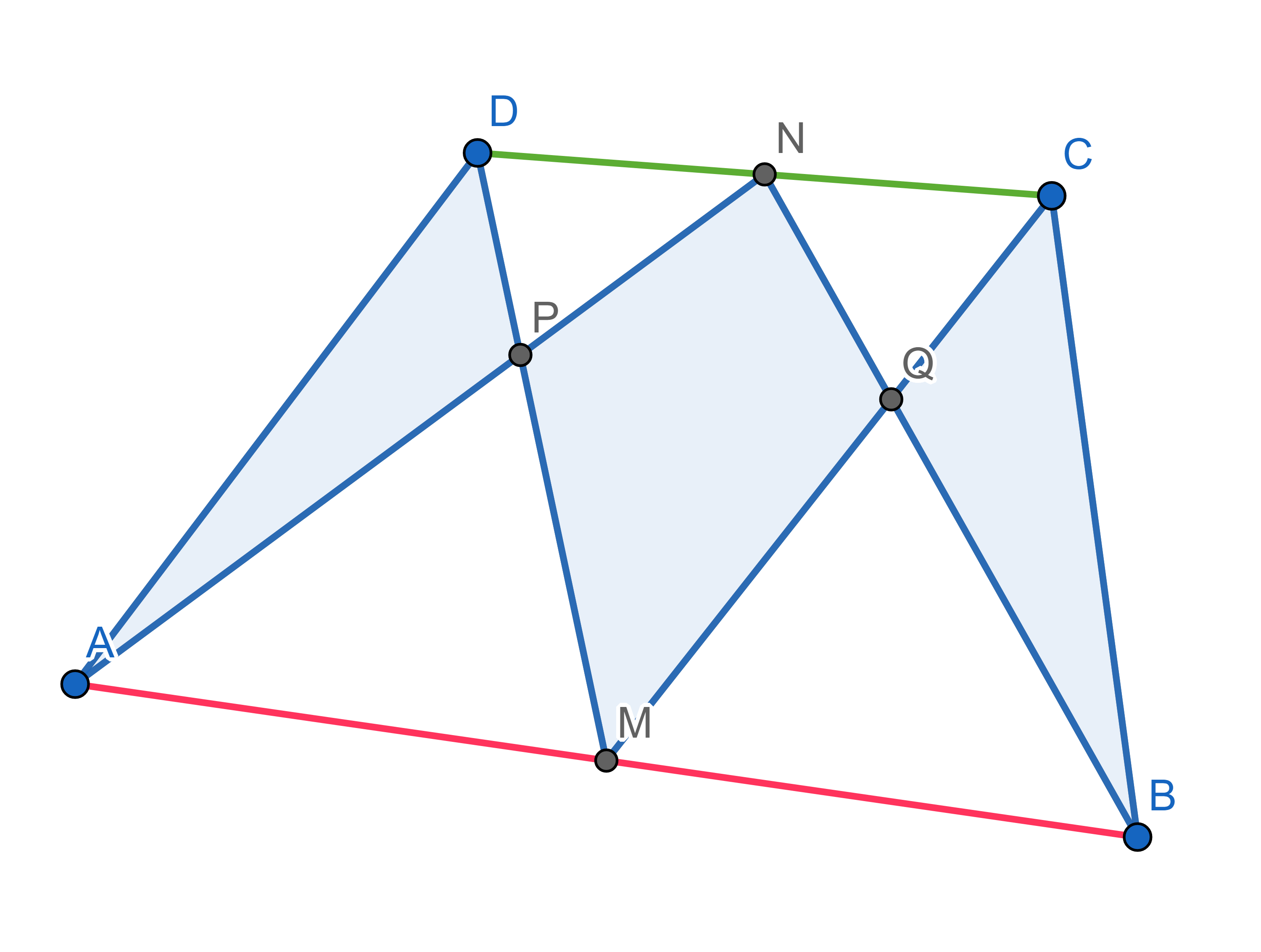
A quadrilateral \(ABCD\) is given. Point \(M\) is a midpoint of \(AB\) and point \(N\) is a midpoint of \(CD\). Point \(P\) is where segments \(AN\) and \(DM\) meet, point \(Q\) is where segments \(MC\) and \(NB\) meet. Show that the sum of the areas of triangles \(APD\) and \(BCQ\) is equal to the area of the quadrilateral \(MQNP\).