Problem #PRU-5216
Problem
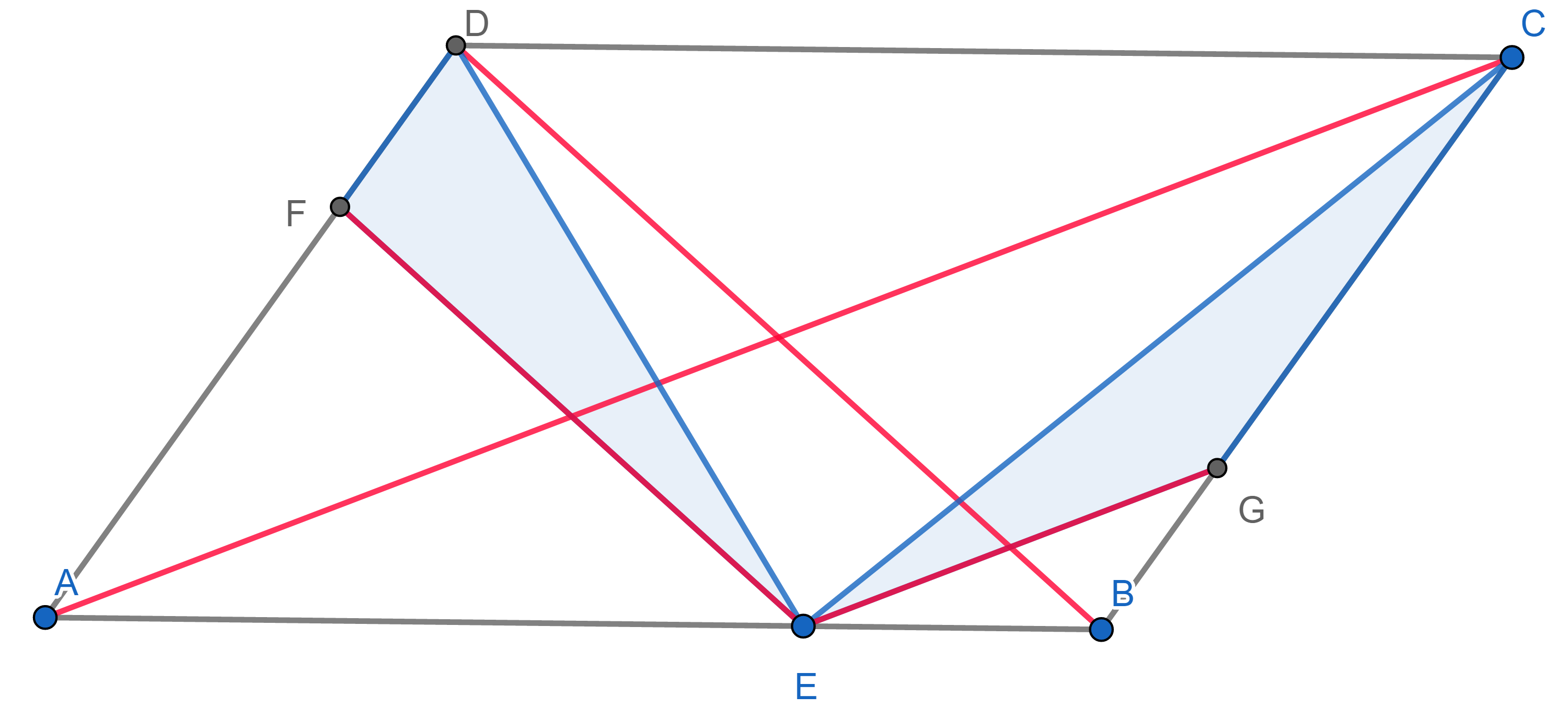
Let \(ABCD\) be a parallelogram. The segment \(EF\) is parallel to the diagonal \(BD\), and the segment \(EG\) is parallel to the diagonal \(AC\). Show that the areas of the triangles \(\triangle EFD\) and \(\triangle EGC\) are equal.
To see the solution register and get verified.