Problem #DES-210924

Problem

Let’s play some games today! We will play a classic game known as nim, which is thought to be one of the oldest games.

Typically people play nim using matchsticks, though stones and coins are popular too. There are a few heaps of matchsticks in nim. Players take turns to remove matchsticks from a heap of their choosing. The player can remove any number of matchsticks they wish from that heap. Whoever has no matchsticks left to take loses.

This following position will be written as \(\text{Nim}(3,3,3)\):

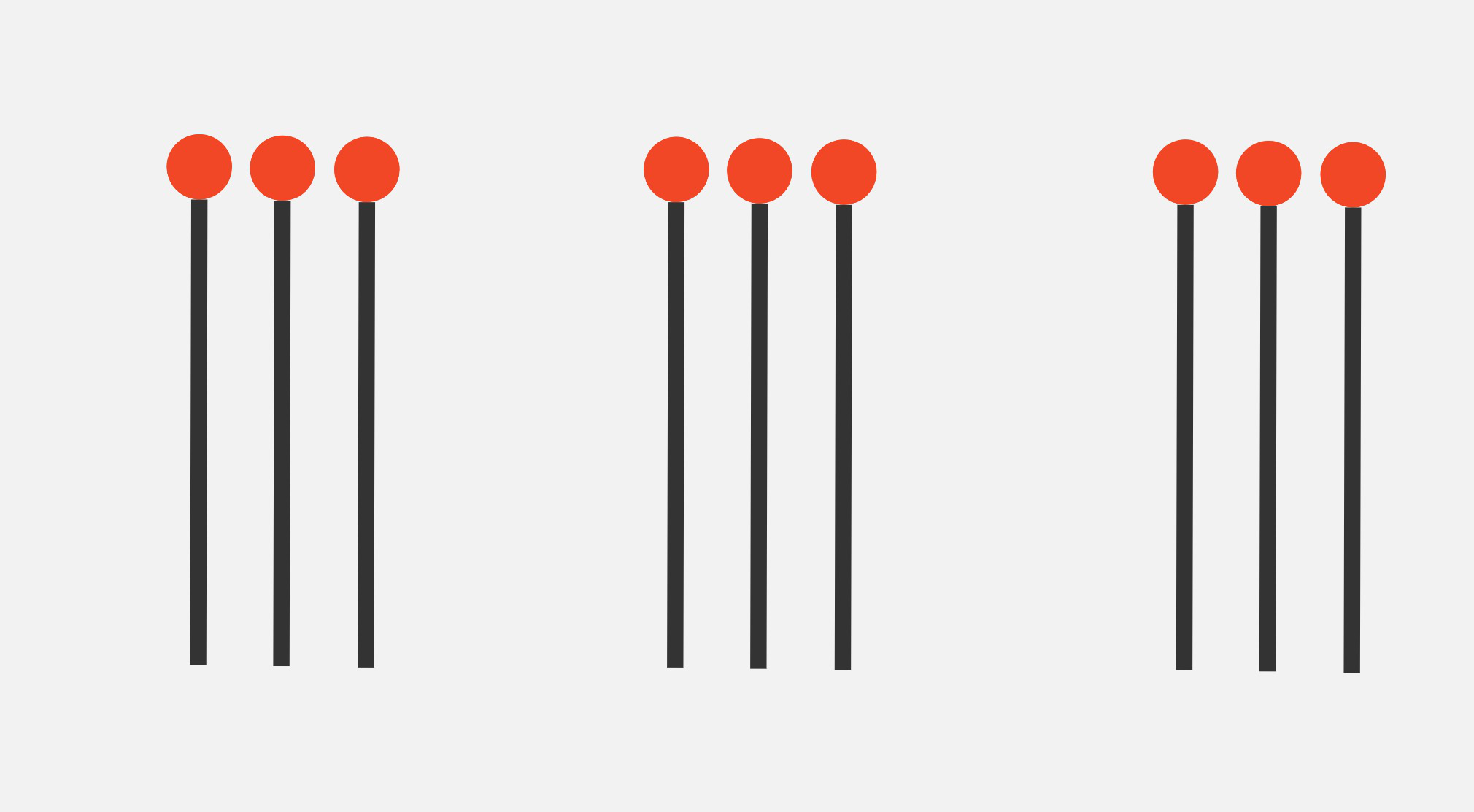
As another example, this is \(\text{Nim}(1,2,3,4)\):

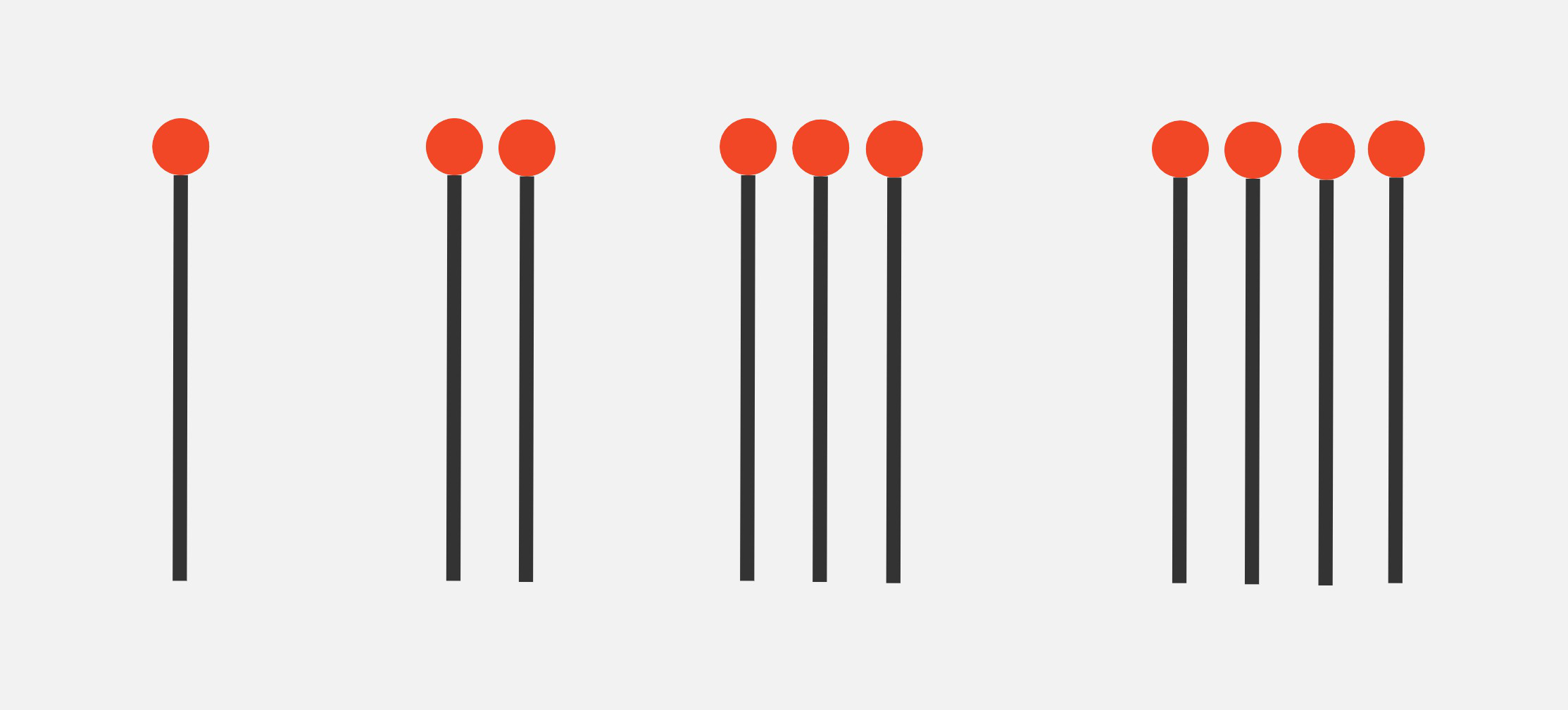
We will omit heaps of size zero, so \(\text{Nim}(3,0,3,0,3)\) is the same as \(\text{Nim}(3,3,3)\).

Nim is important because a large class of games are equivalent to it despite its simple appearance. The interested reader should look up “Sprague-Grundy Theorem".

Let us introduce a few terms that will be helpful for analyzing games. A game \(G\) consists of some positions and a set of rules. A position \(g\) in the game \(G\) is called a winning position if the player starting this turn has a winning strategy. This means as long as the player starting this turn continues to play optimally, the second player has to lose. Conversely, a position \(g\) is a losing position if the player starting this turn has no winning strategy.