Problem #WSP-4005
Problem
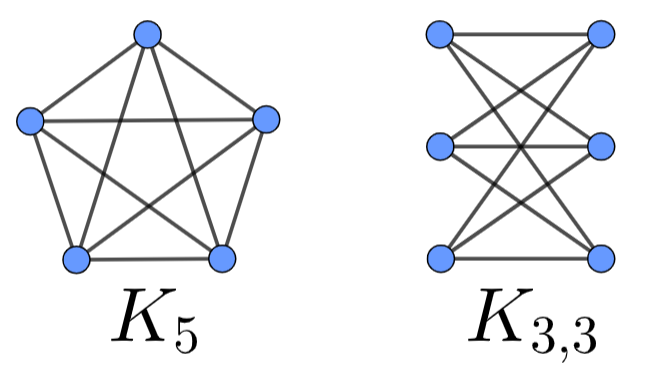
In the picture below you can see the graphs of \(K_5\), the complete graph on \(5\) vertices, and \(K_{3,3}\), the complete bipartite graph on
\(3\) and \(3\) vertices. A theorem states that these
graphs cannot be embedded into plane, namely one cannot draw graphs
\(K_5\) and \(K_{3,3}\) on a plane in such a way that
there are no intersecting edges.
The question is: can you draw the graphs \(K_5\) and \(K_{3,3}\) without intersecting edges on a
torus?
To see the solution register and get verified.