Problem #DES-2-2

Problem

Today we will solve some problems about finding areas of geometric figures. You only need to know how to calculate the area of a rectangle, a triangle and a circle to be able to solve every problem in this set. Here is a brief description of the area formula for each shape.

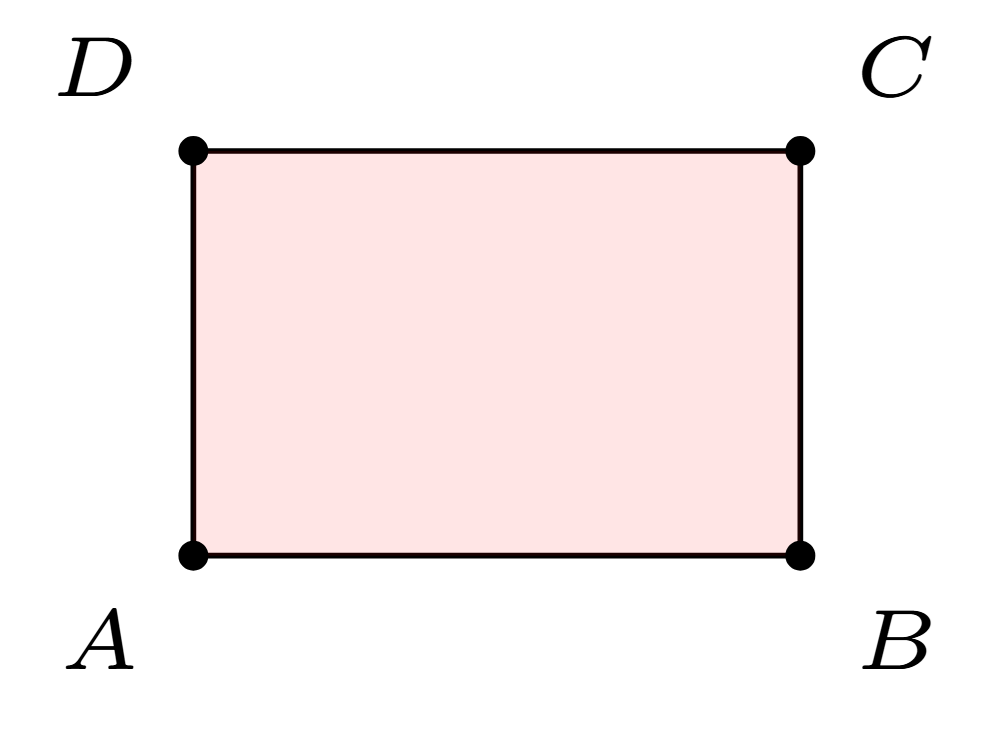
We start with rectangles because they are easy. In the picture below, one way to find the area of the rectangle is to multiple the length of the side \(AB\) by the length of the side \(AD\).

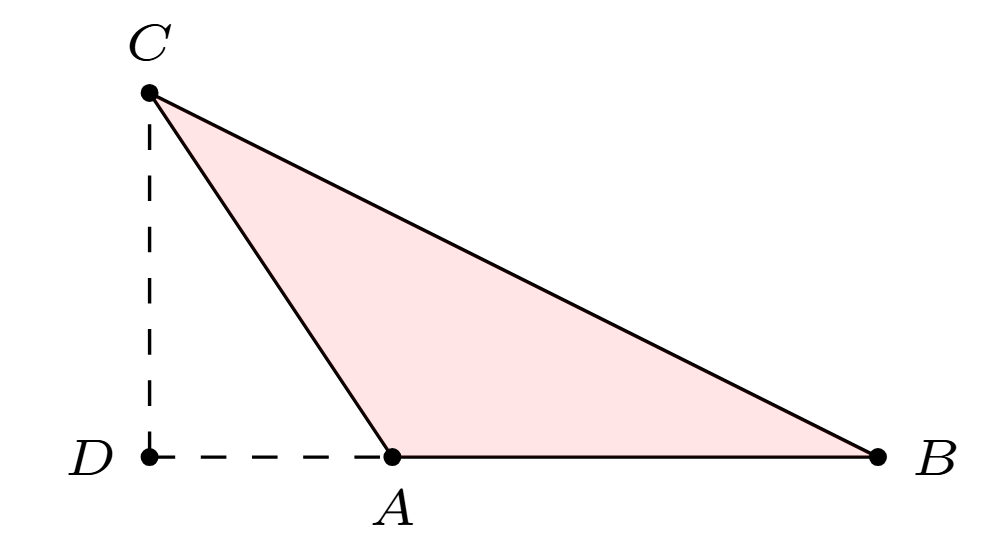
Next we consider the area of a triangle. In general, the area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height (the length of the altitude corresponding to that base). Finding a base and a corresponding altitude is usually straightforward. However, it can be a bit tricky if the altitude lies outside the triangle. See the picture below for one such case. The segment \(AB\) is the base and \(CD\) is the altitude. If the area formula seems hard to believe in this case, please have a look at problem 6.

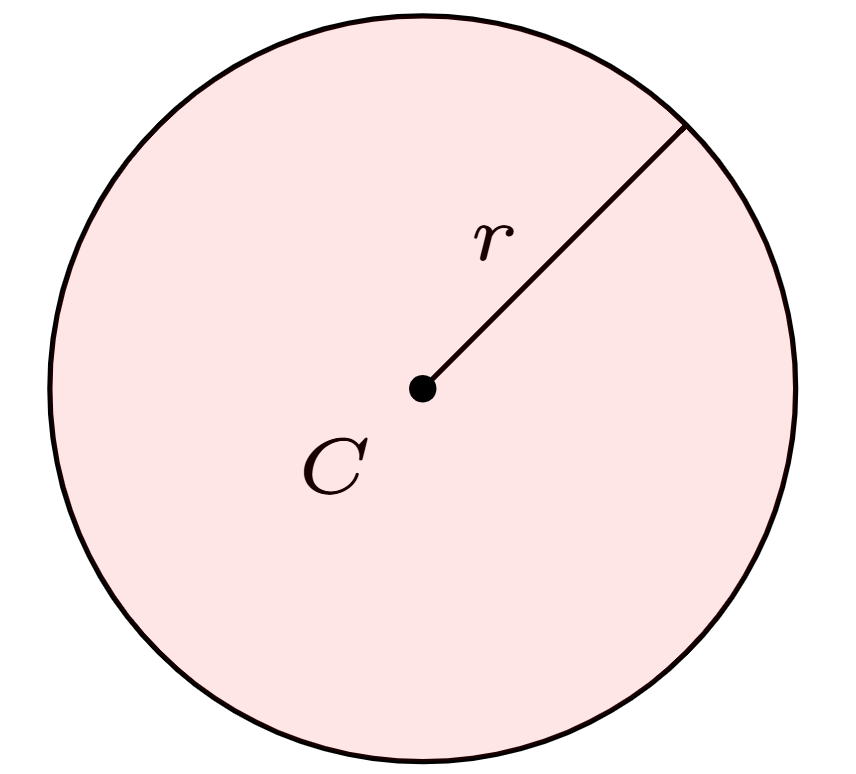
At last, we come to the area of a circle. If a circle has radius \(r\), its area is \(\pi r^2\). A fully rigorous proof requires calculus! The number \(\pi\) is approximately 3.14159 to five decimal points.