Problem #WSP-000175

Problem

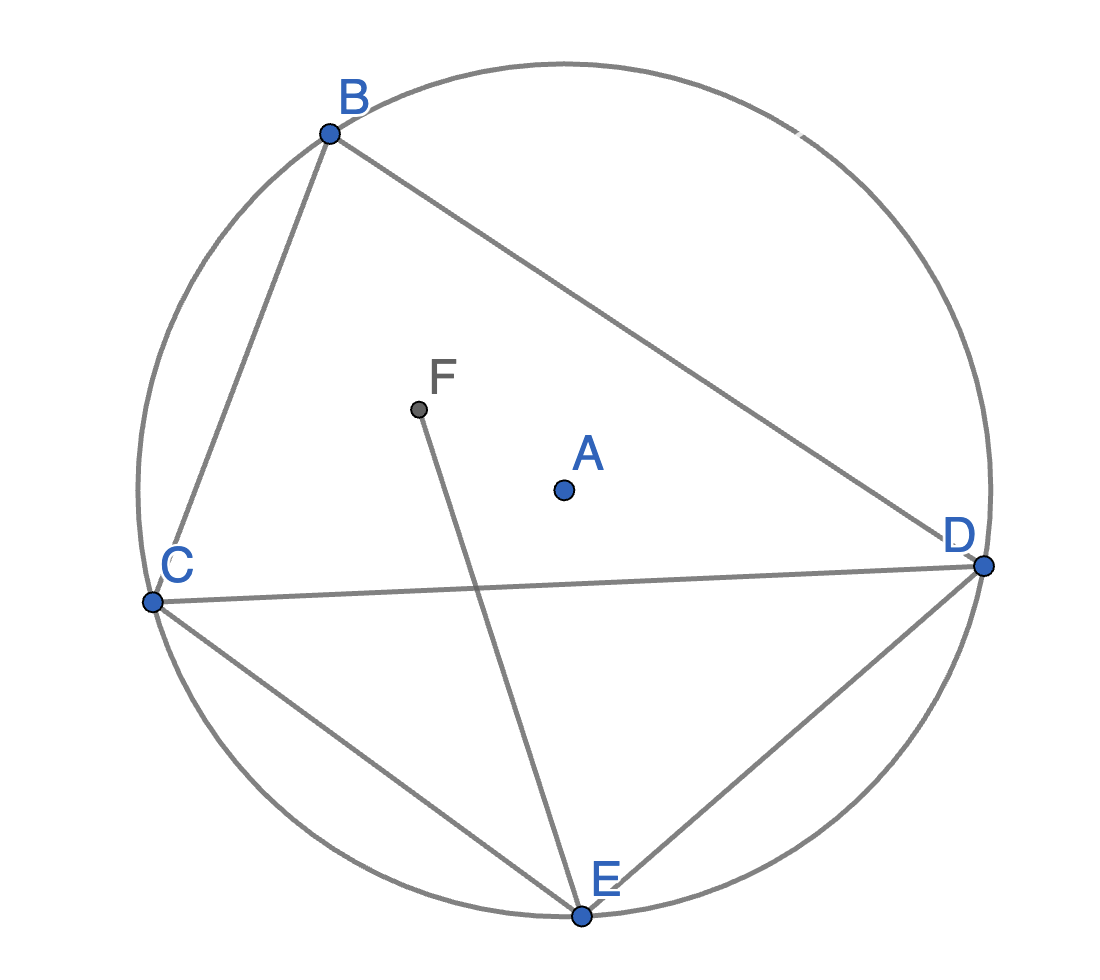
The triangle $BCD$ is inscribed in a circle with the centre $A$. The point $E$ is chosen as the midpoint of the arc $CD$ which does not contain $B$, the point $F$ is the centre of the circle inscribed into $BCD$. Prove that $EC=EF=ED$.