Problem #DES-similarity
Problem
It is often the case in geometric situations that figures look very
similar, but not quite equal. Two polygons on the plane are called
similar if and only if ALL their corresponding angles
are equal AND the ratio between ALL
the corresponding sides is the same.
The relation between the corresponding sides, in our case it’s \(\frac{|AB|}{|IH|}\), is called the
similarity coefficient between the figures. It is common practice to
write vertices of similar figures in the order that respects the
similarity.
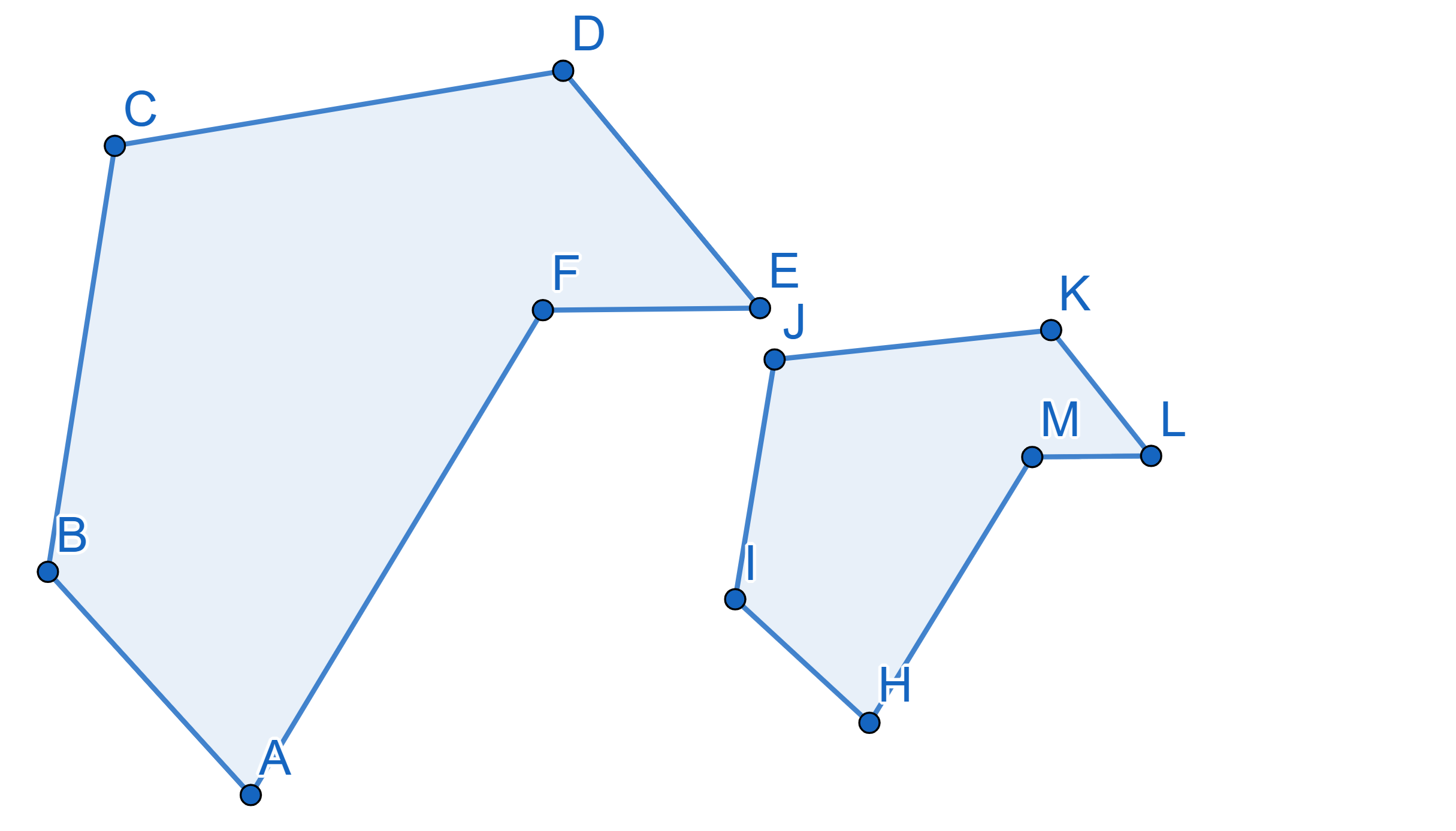
We will find some criteria for determining similarity and apply them to solve problems. The statements of some examples and problems may be helpful for problems coming after them!
To see the solution register and get verified.