Problem #DES-010225

Descriptions
 10–14

Problem

Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
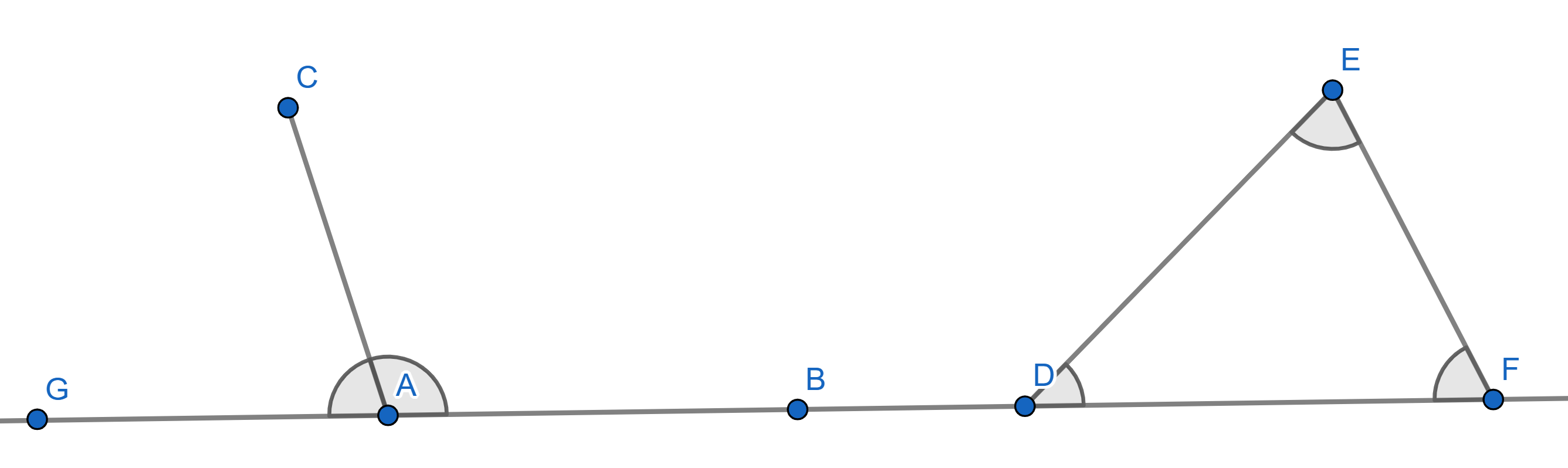
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).

image

3. Two triangles are said to be “congruent" if ALL of their corresponding sides and angles are equal.
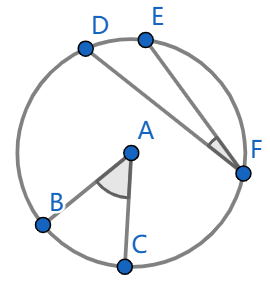
The following terminology will also be quite helpful. In the picture below, the points \(B\) and \(C\) lie on the circumference of the circle while the vertex \(A\) lies at the centre of the circle. We say that the angle \(\angle BAC\) is a central angle. The angle \(\angle DFE\) is called an inscribed angle because the vertices \(D\), \(F\) and \(E\) all lie on the circumference of the circle.

image