Problem #WSP-5297

Problem

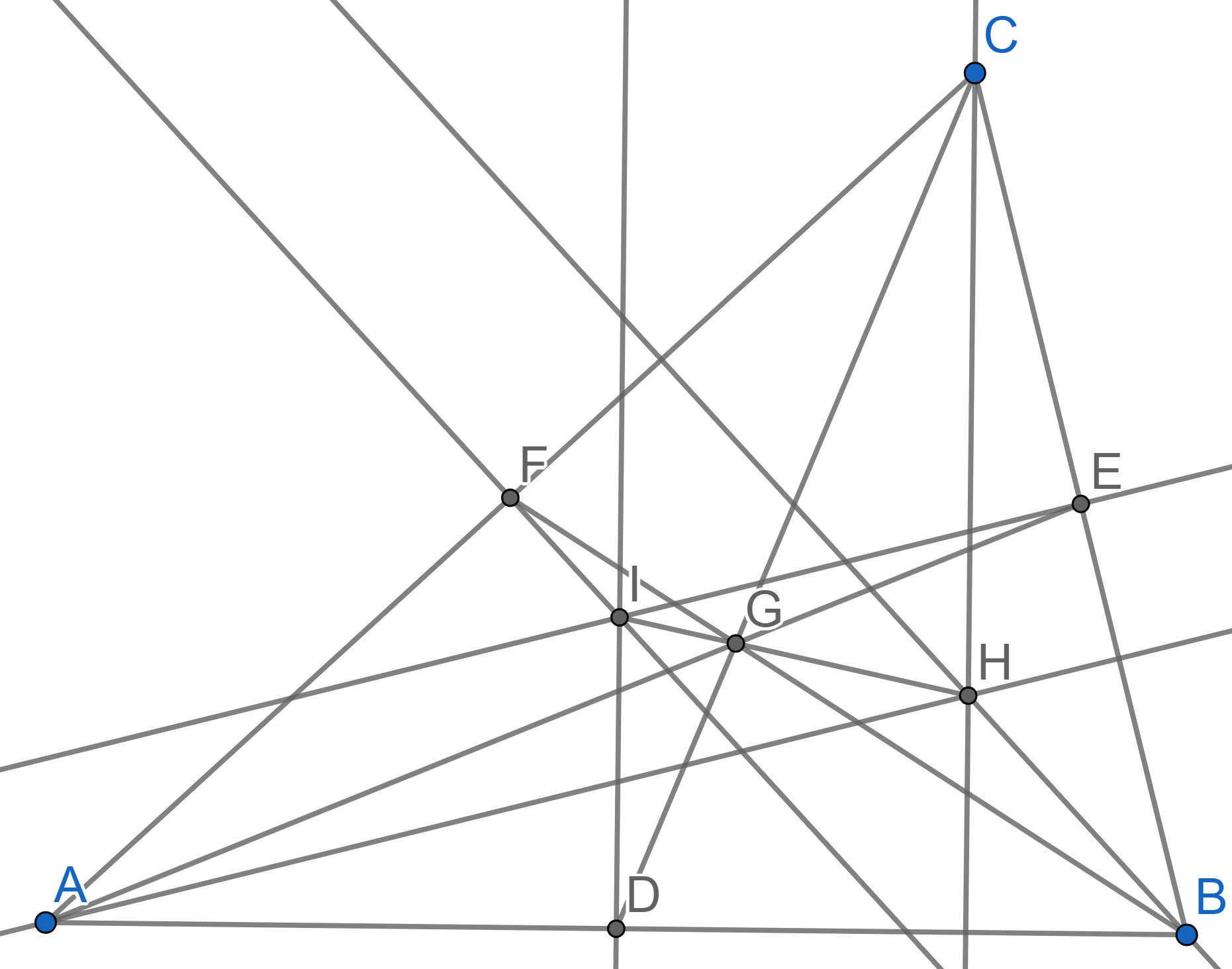
Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\), the point \(H\) is the point of intersection of all heights, the point \(I\) is the center of the circumscribed circle for \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and the ratio \(IG:GH = 1:2\).