Problem #DES-pythag

Problem

Today we will focus on applications of Pythagorean theorem, in geometry and number theory. This famous and ancient theorem states that in a right triangle, the area of a square build on a hypothenuse (the longest side) is a sum of areas of squares build on the other two sides. \[a^2 + b^2 = c^2\]

There are over a 100 proofs of Pythagorean theorem, a quite simple one is visible below:

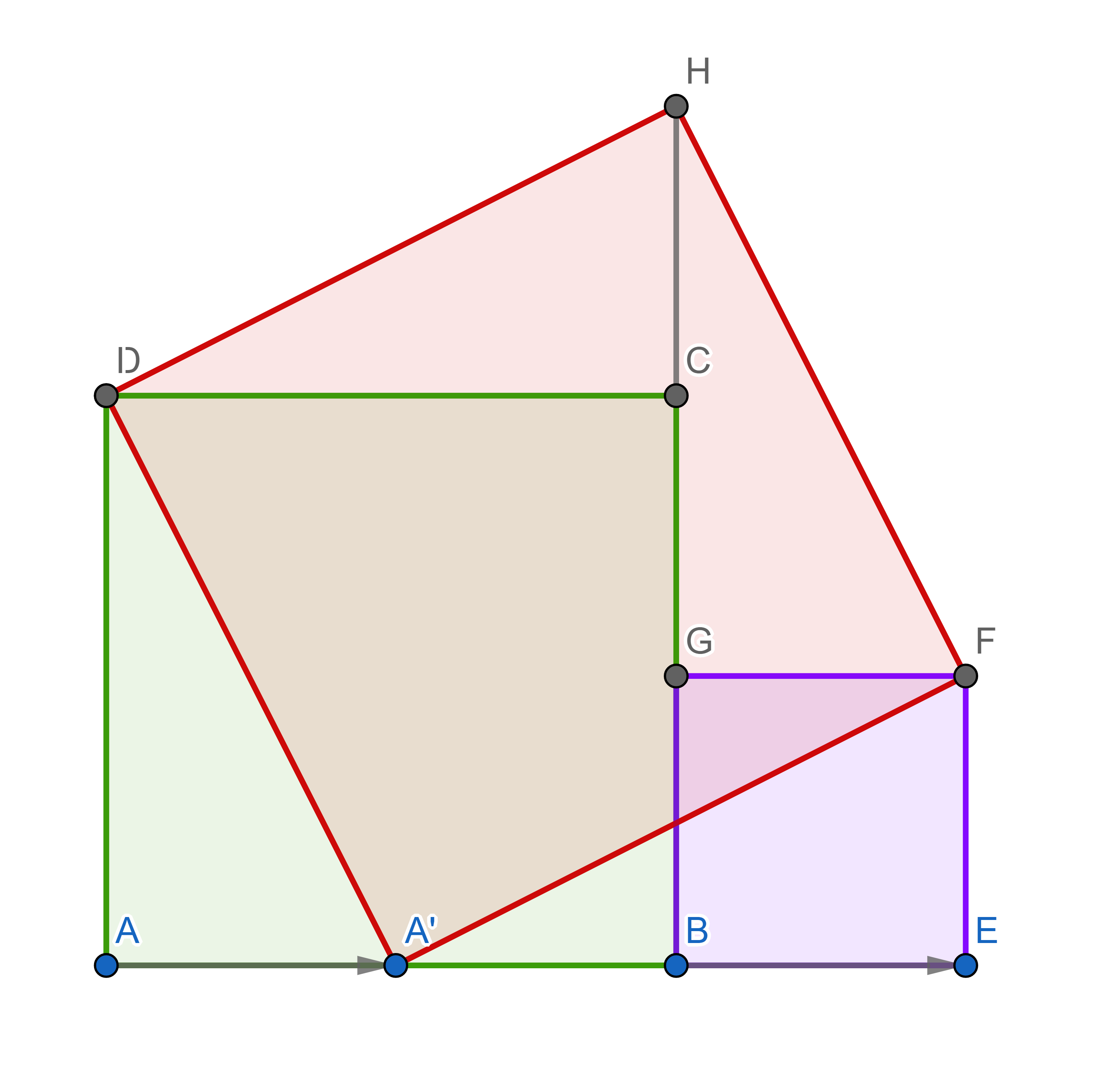
Four right triangles in this picture are identical: \(\triangle A A' D, \triangle EFA', \triangle GFH\) and \(\triangle CHD\). By moving the triangles around you can see that the large red square has the same area as the sum of areas of the other two squares, violet and green.

Today’s session is not only about geometry, we will also learn something about the equation \(a^2 + b^2 = c^2\), where all the numbers \(a,b,c\) are integers.