Problem #WSP-000400

Problem

The picture below shows the ‘hockey-stick’ identity in Pascal’s triangle.

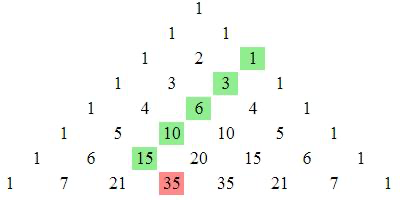
It says that if you start one of the diagonals formed of \(1\)s at the edge, then follow the numbers diagonally in one direction (e.g. left in the picture) and then change direction on your final turn (right in the picture), then the sum of the all but the last number is equal to the last number.

Prove this is true. Written algebraically, \[\binom{r}{r}+\binom{r+1}{r}+...+\binom{n-1}{r}+\binom{n}{r}=\binom{n+1}{r+1},\] where \(0\le r\le n\).