Problem #WSP-5333

Problems Graph Theory
 10–13  4.0

Problem

Sperner’s lemma in dimension \(2\).
Subdivide a triangle \(ABC\) arbitrarily into a triangulation consisting of smaller triangles meeting edge to edge. Define Sperner coloring of the triangulation as an assignment of three colors to the vertices of the triangulation such that:

  • Each of the three vertices \(A, B,\) and \(C\) of the initial triangle has a distinct color

  • The vertices that lie along any edge of triangle \(ABC\) have only two colors, the two colors at the endpoints of the edge. For example, each vertex on \(AC\) must have the same color as \(A\) or \(C.\)

Here is an example of Sperner’s triangulation

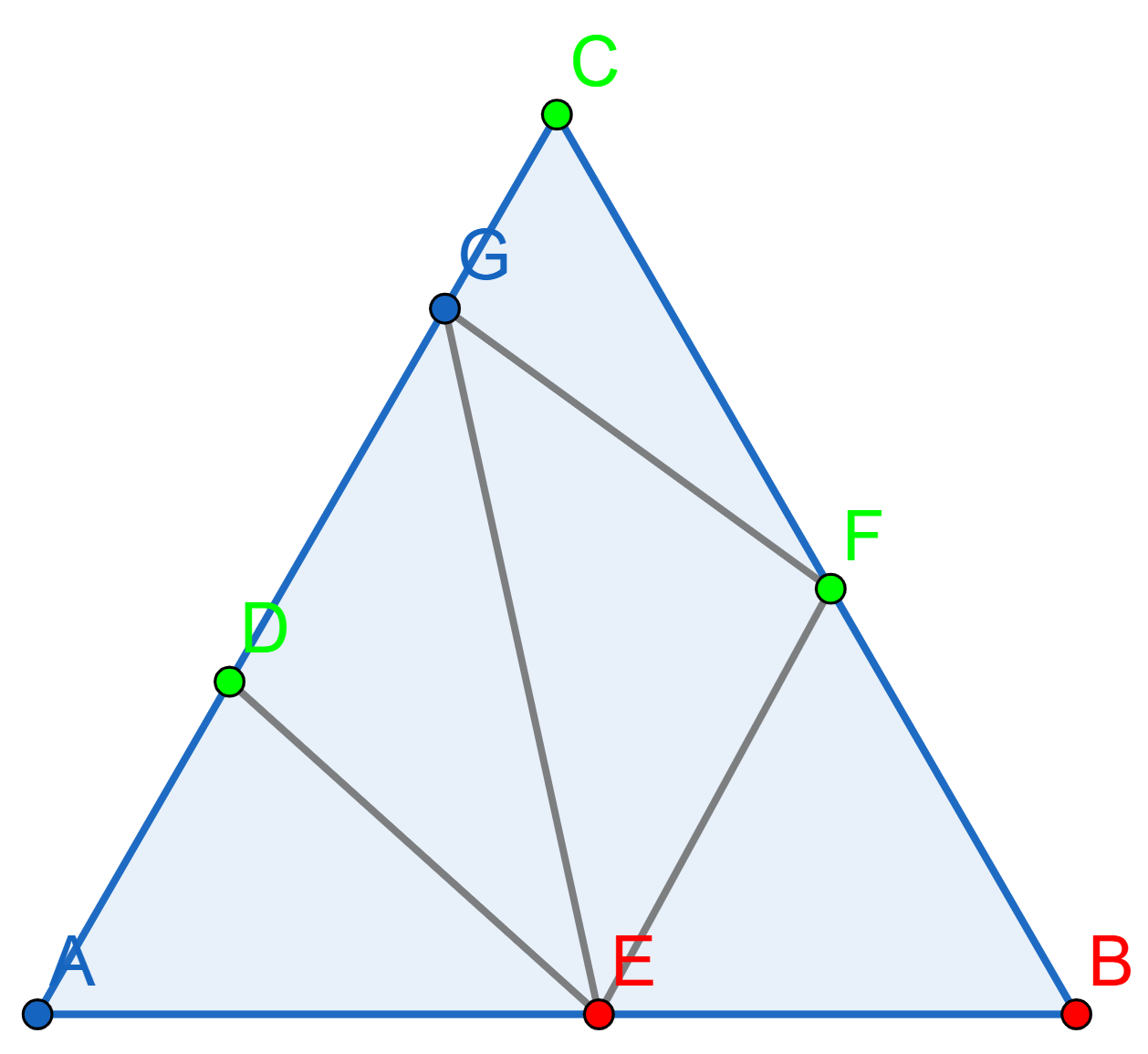
image

Prove that every Sperner coloring of every triangulation has at least one "rainbow triangle", a smaller triangle in the triangulation that has its vertices colored with all three different colors. More precisely, there must be an odd number of rainbow triangles.