Problem #WSP-000474
Problem
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).
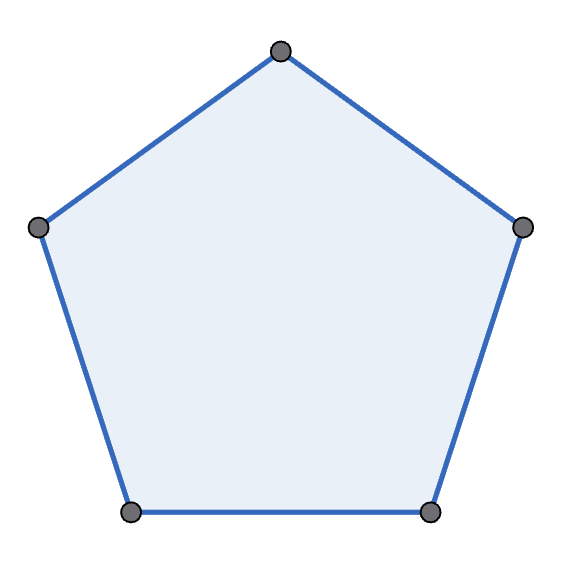
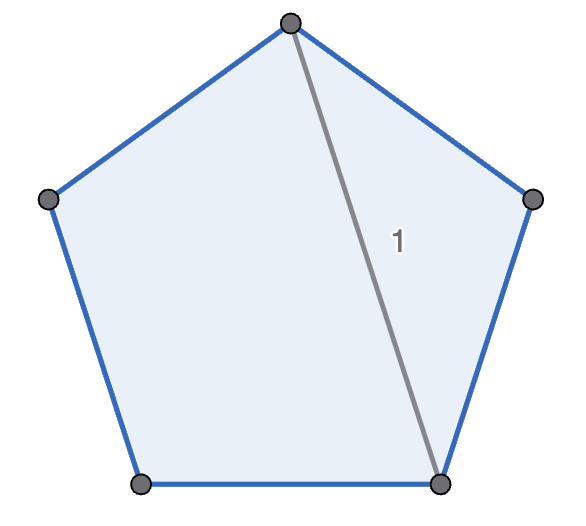
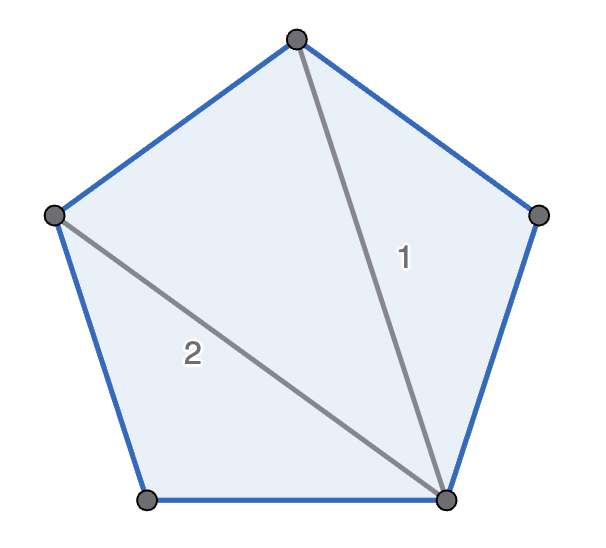
To see the solution register and get verified.