Problem #DES-ramsey

Descriptions
 10–14

Problem

You may have seen the first example (seen below) previously. Before we get to that, let’s introduce some notation. We write \(K_n\) for the _complete_ graph on \(n\) vertices - that is, every possible edge is present.

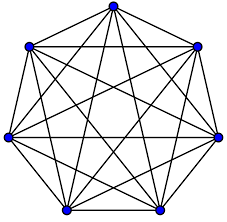
image

Note that edges don’t have a direction, and are between pairs of different vertices. Ramsey theory looks at what happens when we colour every edge in \(K_n\) either red or blue. Are we guaranteed a red \(K_3\) subgraph? No, because we could just colour every edge in \(K_n\) blue. Instead, we ask if we are guaranteed a red \(K_3\) or a blue \(K_3\) subgraph? It turns out yes, so long as \(n\) is big enough.

We can then look at extensions to this problem. We write \(R(s,t)\) for the least number \(n\) such that whenever you colour the edges of \(K_n\) in red or blue, then you’re guaranteed a red \(K_s\) or a blue \(K_t\). By least \(n\), this means that there’s a colouring of the edges of \(K_{n-1}\) with no red \(K_s\) or blue \(K_t\).