Problem #WSP-5561

Problem

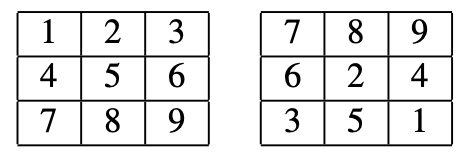
Consider the two following grids. We consider two of the little squares to be a neighbor if they share a side (so that diagonals don’t count as neighbours). You are allowed to choose any two neighbouring little squares and add the same whole number to both squares. Show that by repeating this step, you cannot turn the first grid into the second one.