Problem #DES-08Homlvl2

Descriptions
 10–14

Problem

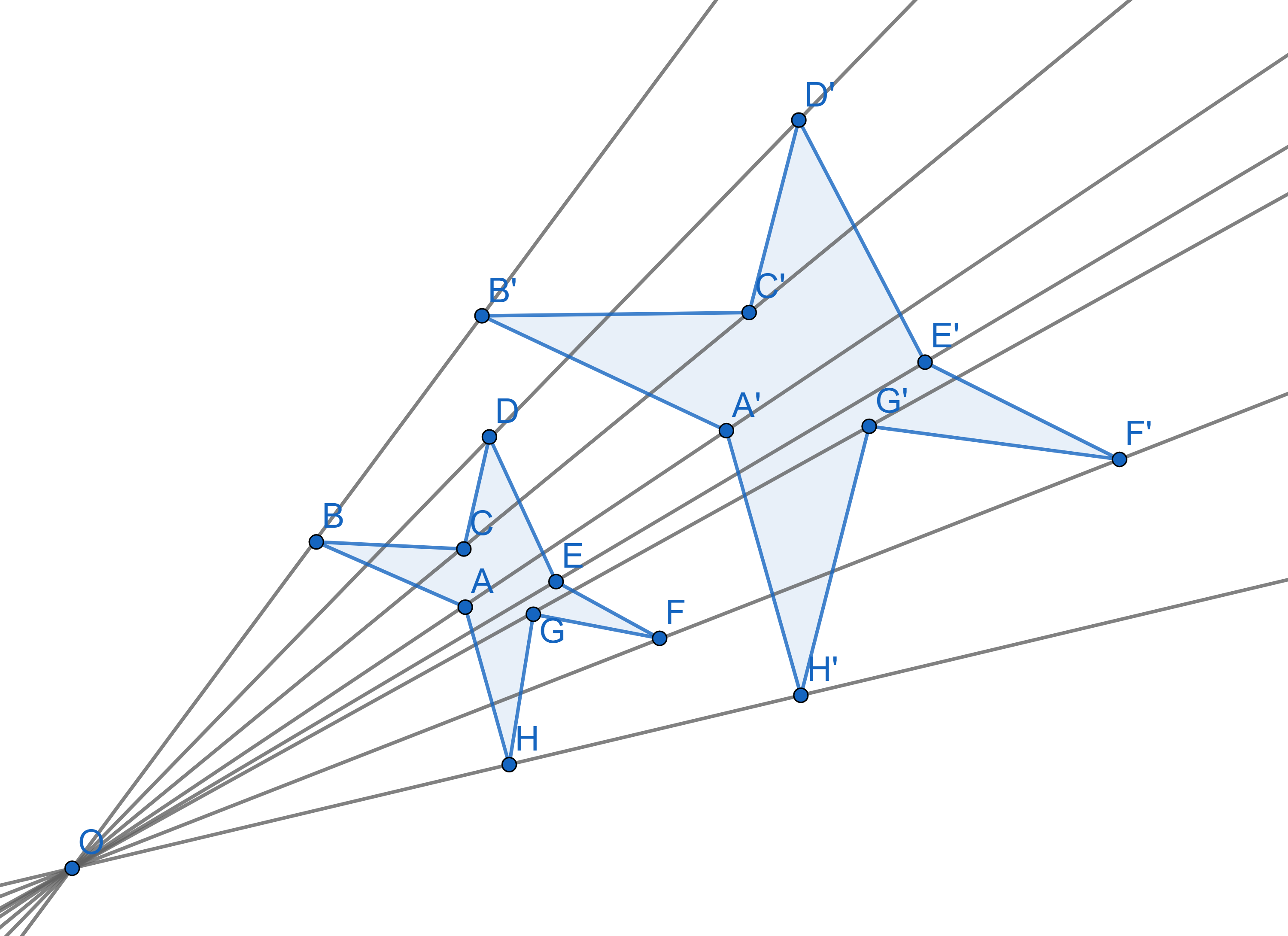
Sometimes geometric problems are solved using a variety of plane transformations. One of such transformations is called Homothety. It requires the following data:

  1. The center of homothety: a point on the plane, we will usually denote it as \(O\).

  2. The koefficient of homothety: a real number, we will denote it as \(k\).

The plane transformation is described in the following way: every point \(X\) on the plane is sent to a point \(X'\) with the following properties: The points \(O, X, X'\) lie on one line, in that exact order for a coefficient \(k \geq 1\). The distance is defined in the same way for any real coefficient, but he order of the points on the line changes in the following way:

  • For \(0<k \leq 1\) the order is \(O,X',X\);

  • For \(k\leq 0\) the order is \(X',O,X\).

The distance \(OX' = kOX\).

image