Problem #WSP-5602

Problem

Let \(ABCD\) be a quadrilateral whose diagonals intersect at a point \(E\).

Consider the four triangles \(ABE\), \(BCE\), \(CDE\), and \(ADE\). For each triangle, draw its medians, and let \(K\), \(J\), \(M\), and \(L\) be the points where the medians intersect in the triangles \(ABE\), \(BCE\), \(CDE\), and \(ADE\), respectively.

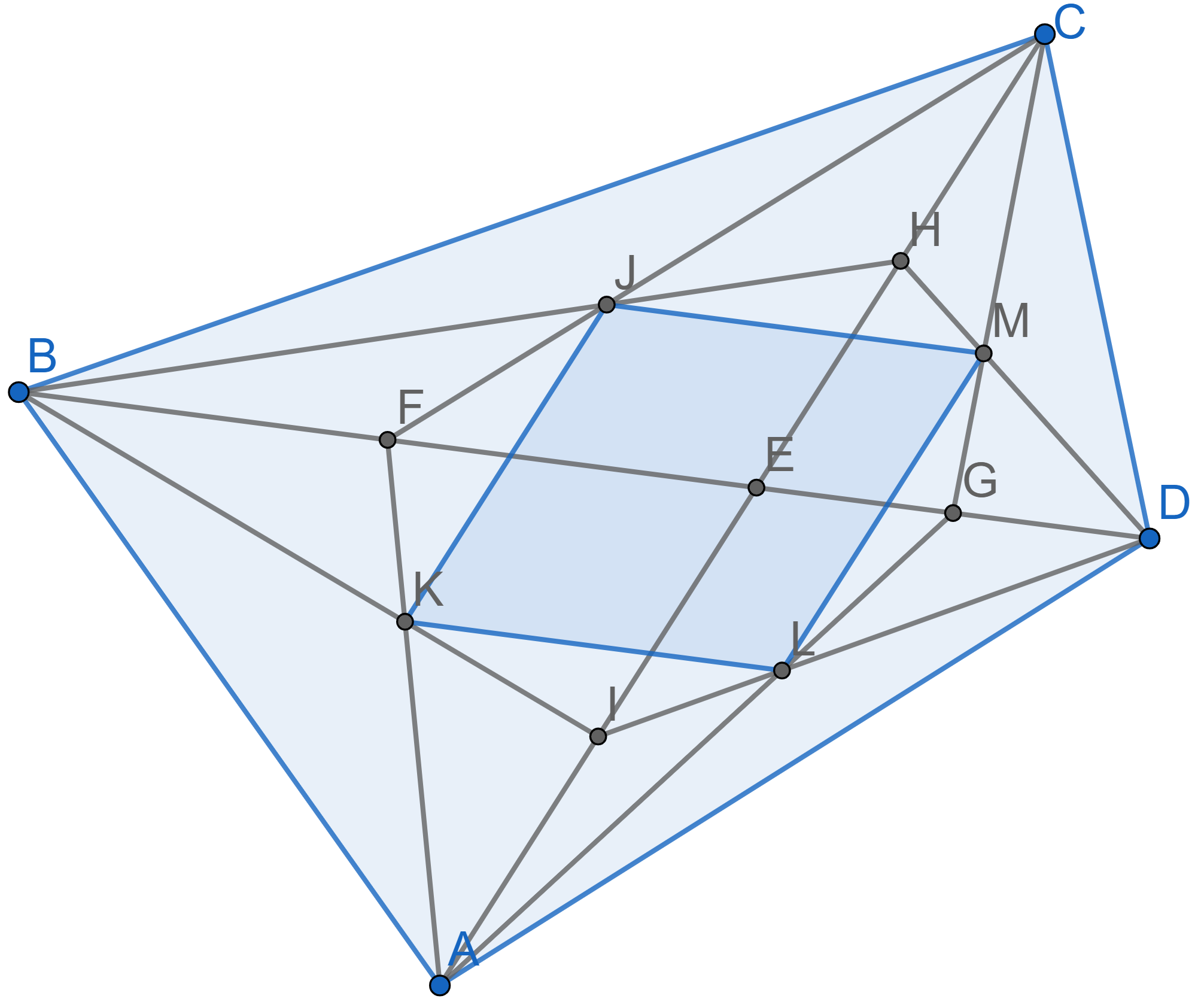
Prove that the quadrilateral \(KJML\) is a parallelogram.

You may wish to use the fact that the point of intersection of the medians of any triangle divides each median in the ratio \(2:1\), counting from the vertex, but if you use this fact, you should prove it.