Problem #DES-310126

Problem

The inclusion–exclusion principle is a very useful counting tool. It is based on the simple idea of counting too much and then fixing the mistake.

Suppose there are two properties \(A\) and \(B\) that objects may or may not have (for example, a sticker can be shiny or round). Say there are \(a\) objects with property \(A\) and \(b\) objects with property \(B\). We ask: “How many objects have at least one of the two properties?”

If objects can have property \(A\) or property \(B\), but not both, then the answer is simply \(a+b\). However, if objects can have both properties, then \(a+b\) counts those objects twice. In the picture below, objects are shown as red dots, and the numbers show how many times each region is counted.

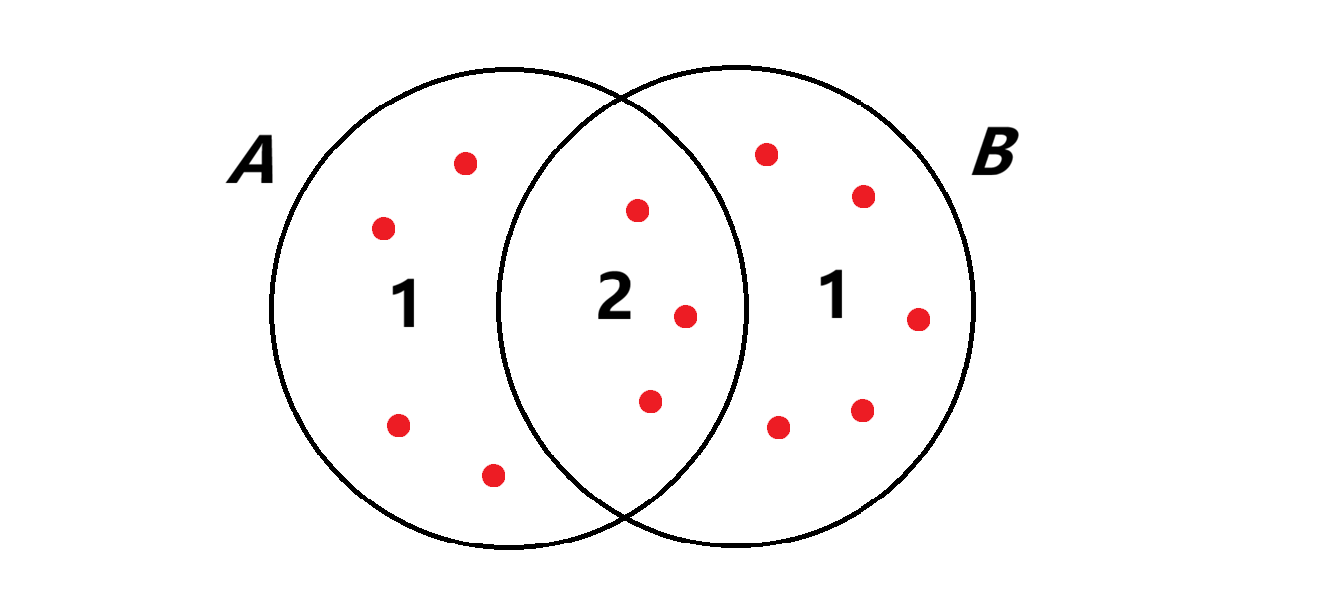
Let the number of objects with both properties be \(x\). These objects are counted twice, so to fix this we subtract \(x\). The correct total is therefore \(a+b-x\).

Now let us think about what happens with three properties \(A,B,C\). Suppose there are \(a\) objects with property \(A\), \(b\) with property \(B\), and \(c\) with property \(C\). The number \(a+b+c\) again overcounts. A picture helps us see by how much.

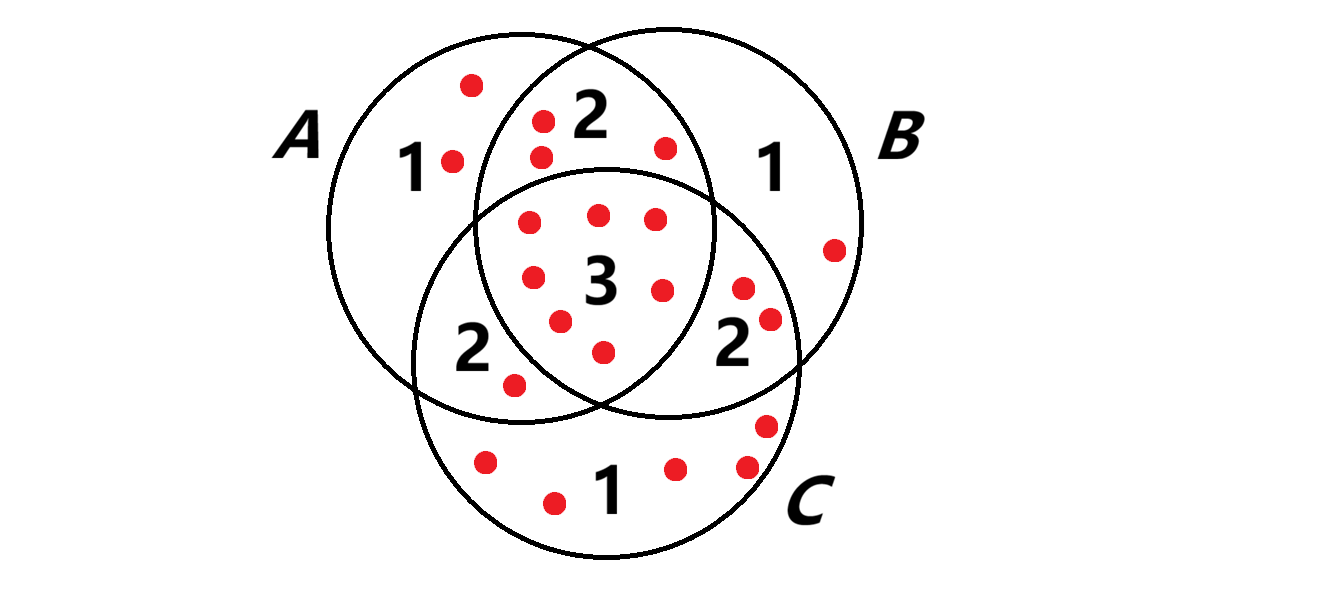
Let \(x\) be the number of objects with properties \(A\) and \(B\), \(y\) the number with \(B\) and \(C\), and \(z\) the number with \(A\) and \(C\). As before, we subtract \(x\), \(y\), and \(z\). This gives \(a+b+c-x-y-z\). But now we have gone too far.

Let \(w\) be the number of objects with all three properties. These were removed once too often, so we add \(w\) back. The correct total is \(a+b+c-x-y-z+w\).

We do not have to stop at three properties, but the formulas get longer. The key idea is always the same: notice when you have counted something too many times or too few times, and then correct it. Let us now look at some examples to see this idea in action.