Problem #DES-310126
Problem
The inclusion-exclusion principle is an immensely useful counting tool. This stems from the intuitive idea of overcounting and undercounting.
Suppose there are two properties \(A\) and \(B\) that some objects may or may not satisfy. Let us say that there are \(a\) objects with property \(A\) and \(b\) objects with property \(B\). We can ask, “how many objects have at least one of the two properties?"
If the objects can have either property \(A\) or \(B\), but not both, then \(a+b\) is correct count. However, if objects can have both property \(A\) and \(B\), then \(a+b\) counts those with both properties twice. In the picture below, objects are represented as red dots and the number indicate how many times we have counted the objects in that region.
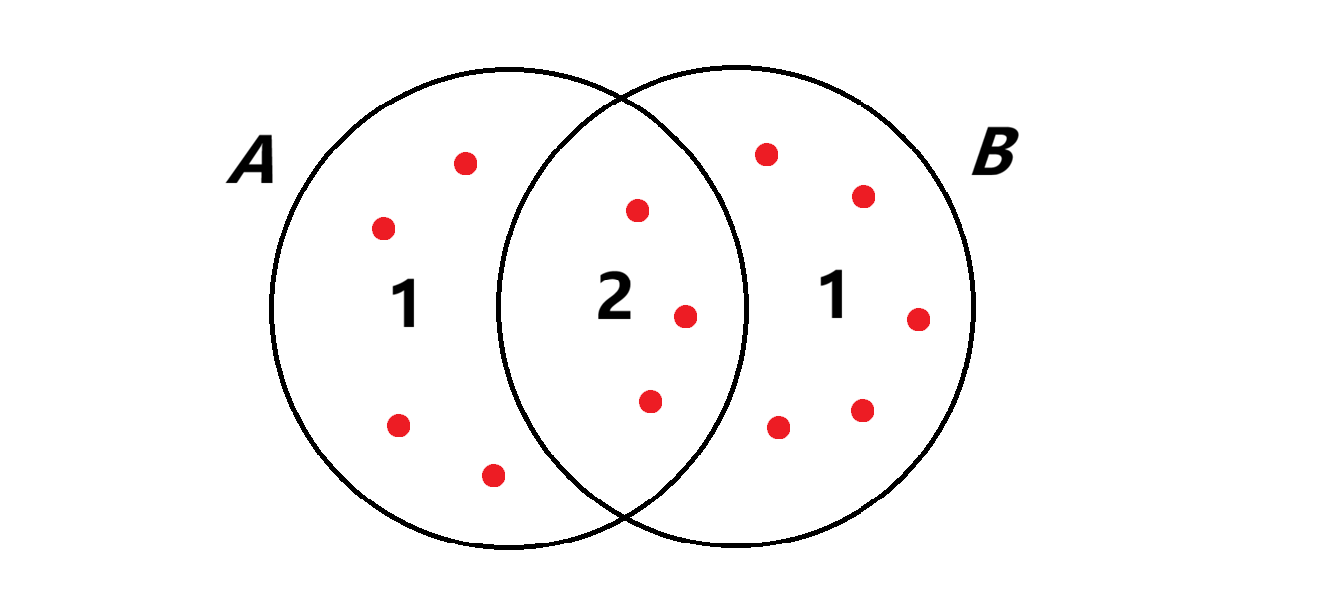
Let the number of objects having both properties be \(x\). Here we are clearly counting these object twice. To get the correct count, we need subtract \(x\). So the total number should be \(a+b-x\).
Let us also think about what may have if we have three properties \(A,B,C\). Let us say that there are \(a\) objects with property \(A\), \(b\) objects with property \(B\) and \(c\) objects with property \(C\). The number \(a+b+c\) again overcounts. By how much? Drawing a cartoon picture is again helpful.
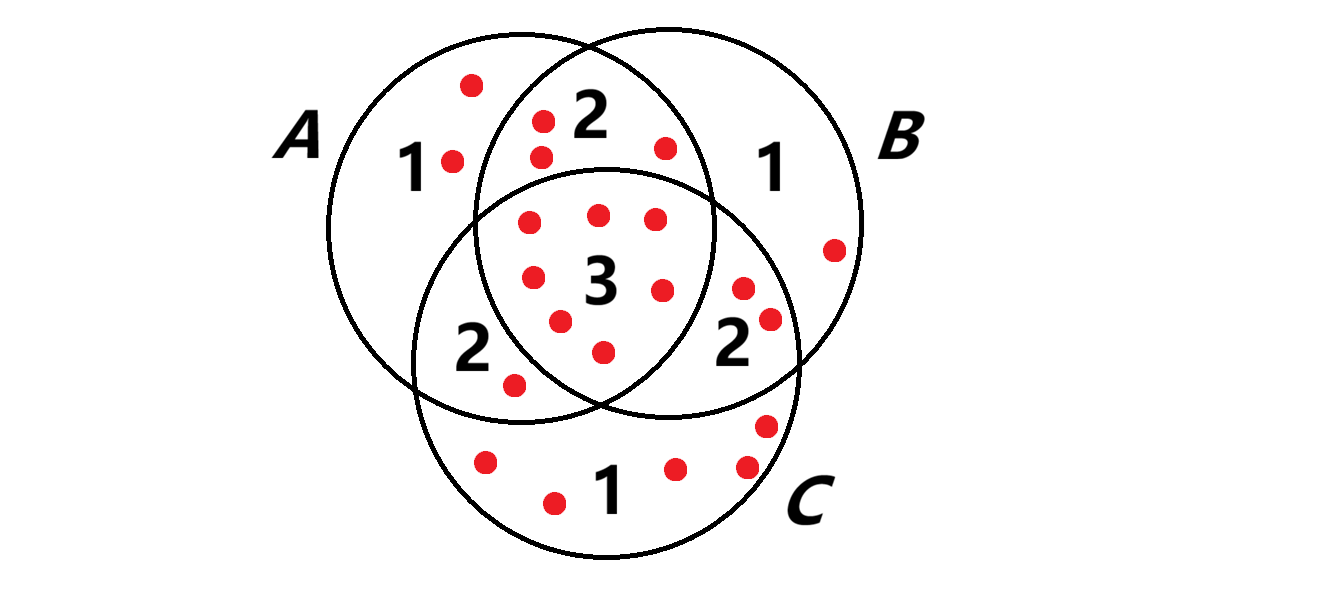
Let \(x\) be the number of objects with property \(A\) and \(B\), \(y\) the number of objects with property \(B\) and \(C\), \(z\) the number of objects with property \(A\) and \(C\). As before, we want to subtract \(x\) to correct for the number of objects with property \(A\) and \(B\). Similarly, we should subtract \(y\) and \(z\). So is \(a+b+c-x-y-z\) the correct count?
Here run into the opposite problem. We are not counting the number of objects with all three properties. Here is a cartoon for \(a+b+c-x-y-z\):

Let \(w\) be the number of objects with all three properties. The correct count is \(a+b+c-x-y-z+w\).
Of course, we do not have to stop at three properties! However, the formulas become longer to write down. The important part is to understand when you are overcounting or undercounting and how to correct for them. For the moment, let us have a look at some examples, which should make the reasoning and formula easier to digest.