Problem #PRU-53749

Problem

For a trapezium \(ABCD\), let \(E\) be the point of intersection of the sides \(AB\) and \(CD\), and let the point \(G\) be the point of intersection of the diagonals of the trapezium. Finally, let \(F\) amd \(H\) be the midpoints of the sides \(BC\) and \(AD\) respectively.

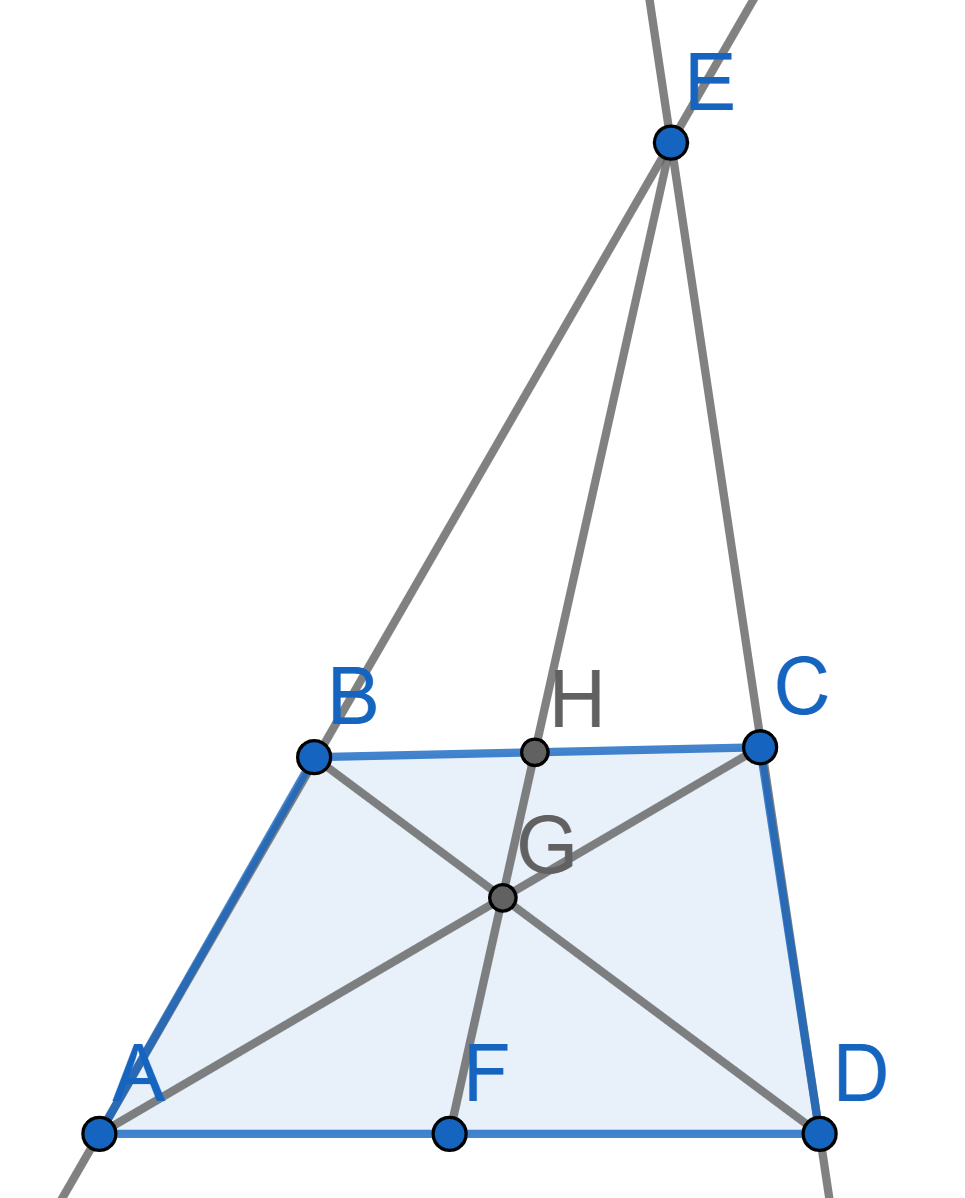
Prove that the points \(E,F,G,H\) lie on one line.