Problems
So far we have discussed polynomials in one variable, i.e: with only an \(x\) as our variable. We can however, include as many as we want. For example, we can talk of a polynomial such as \[P(x,y)=x^2-y^2,\] where both \(x\) and \(y\) are variables. This is an example of an antisymmetric polynomial, which means that \(P(x,y)=-P(y,x)\) (i.e: switching \(x\) for \(y\) gives the original polynomial with a minus sign). Conversely, a polynomial \(Q(x,y)\) such that \(Q(x,y)=Q(y,x)\) is called symmetric. Show that every antisymmetric polynomial \(P(x,y)\) can be factored as \[P(x,y)=(x-y)Q(x,y),\] where \(Q(x,y)\) is a symmetric polynomial.
Solve the equation \[\left(x^2-3x+3\right)^2-3\left(x^2-3x+3\right)+3=x\]
Find all integer solutions to \(x^2+y^2-1=4xy\).
Often in maths we want to prove statements of the form “If A, then B.” For example: “If a number is divisible by \(4\), then it’s even.”
Usually, we prove such statements using something called a direct proof. In the example above, a direct proof would start by imagining we have some number — we don’t know which one — but we know it has the property “divisible by \(4\)”, and then using this information to work out that the number must be even.
However, this kind of direct reasoning can sometimes be tricky. Luckily, there’s another way! The idea is that a statement of the form “If A, then B” means exactly the same thing as “If not \(B\), then not \(A\).”
This second way of writing it is called the contrapositive, and we call “not \(B\)” the negation of \(B\). Here’s an everyday example: “If it rains, then I take my umbrella." is exactly the same as saying “If I don’t take my umbrella, then it’s not raining."
When we use this method in maths, we often say we’re proving by contrapositive: instead of proving “If \(A\) then \(B\)”, we prove “If not \(B\) then not \(A\).” Using this idea, to prove the example above, it would be the same as to prove the statement: ”If a number is not even, then it’s not divisible by \(4\)".
We sometimes write “If \(A\) then \(B\)” as \(A \implies B\), which is pronounced “\(A\) implies \(B\)”. Its contrapositive is: \(\text{not }B \implies \text{not }A.\) This way of thinking often makes a proof much simpler. Let’s see some examples to learn how to use this method.
One of the most powerful ideas in mathematics is that we can use letters — like \(a, b, n\) or \(x\) — to stand for numbers, shapes or other things. When we do this, we can reason about all such possible objects at once, without knowing exactly which number or shape we are really dealing with.
For example, the statement \[\text{``Let } a,b \text{ be numbers. Then } a+b=b+a."\] is true no matter what numbers \(a\) and \(b\) are. It tells us all of the following at the same time: \[3+5=5+3, \qquad (-10)+(-2)=(-2)+(-10), \qquad 7+0=0+7,\] and many more.
The rule \(a+b=b+a\) does not depend on the “three-ness” of \(3\) or the “five-ness” of \(5\) — it works for any numbers. Of course, we could not let \(a\) be a triangle and \(b\) be a tiger, because we do not know what it means to add a triangle to a tiger! Our rules only apply to objects for which the operations make sense.
This way of using symbols to express rules and patterns is what we call algebra. As long as we follow the rules that numbers follow, our reasoning will stay true. Today we will practise using these symbols to work with the algebra of numbers — it may take effort, but it is an important skill that will help you a lot in your mathematical journey.
One of the most important tools in maths is the Pigeonhole Principle.
You may have already met it before, but if not, let’s recap it quickly.
Simply put: the Pigeonhole Principle states that if you have \(n\) pigeons (or objects) that you want to
place into a number of pigeonholes (or containers) that is strictly
smaller than \(n\), e.g: \(10\) pigeons but only \(9\) pigeonholes, then there will be a
pigeonhole with at least two pigeons. Why is this true? Imagine that
every pigeonhole had at most one pigeon. Since we have \(9\) pigenholes in total, there would be at
most \(9\) pigeons, not \(10\), as we are told. Today we will see how
this principle can be used to solve problems about numbers and their
divisibility properties.
Before we get started, we need to recap a very important concept: if we
have two numbers, say \(a\) and \(b\), we can divide \(a\) by \(b\), and we will obtain a quotient
\(q\) and a remainder \(r\), and write \[a=q\times b + r\] for example: if we
divide \(9\) by \(4\), we can write \(9=2\times 4 + 1\), i.e: the quotient will
be \(2\) and the remainder will be
\(1\). A final key fact that we need to
recap is the following: imagine we want to divide two numbers, for
example \(11\) and \(6\) by the same number, say \(4\). We can write \[11=2\times 4 + 3\qquad \text{and}\qquad 6=1\times
4 + 2\] So we can imagine \(11\)
as two packs of \(4\) little squares
and \(3\) “left over" squares, and
\(6\) as one pack of four little
squares with \(2\) left over squares.
We can combine these \(5\) “left over"
squares into one new pack of four, with now one “left" over square. With
this way of thinking, we see that the remainder of a sum of two
numbers \(a\) and \(b\) is precisely the remainder of the
sum of the remainder of \(a\) plus
the remainder of \(b\).
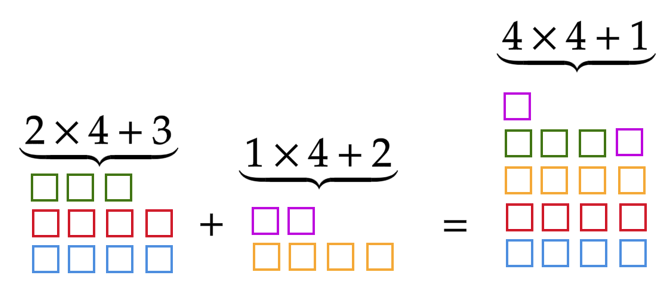
A final remark: in today’s sheet, when we say positive whole numbers, or natural numbers, we will mean the numbers \(1,2,\cdots\)