Problems

Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(4\times 6\) rectangle?

Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(5\times8\) rectangle.

Tile the whole plane with the following shapes:

David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrose looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with this net:

After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:

how can we cut this into three congruent shapes?

A big square was cut into smaller squares. Sebastian used all the pieces and constructed two squares with different side lengths by glueing the pieces together. Show an example of how he could do that.

It was Sebastian’s younger brother who cut the big square in Example 2. Now you need to help him to cut one of the squares (which Sebastian obtained after glueing the pieces) into smaller congruent triangles. But please make sure the elder brother can do the same thing as before: to divide the resulting congruent triangles into two groups and to glue the pieces of each group together to make two squares with different side lengths.

(a) A picnic spot has a form of a 100 m\({}\times {}\)100 m square. Is it possible to partially cover it with non-intersecting square picnic blankets so that the total sum of their perimeters will be greater than 10,000 m?

(b) One sunny day almost every citizen came to the picnic spot from point (a). All of them brought square picnic blankets. In a local newspaper there was mentioned that the total area of grass covered with picnic blankets was greater than 20,000 m\(^2\). Do you think it was possible or did they make a mistake in their computations?

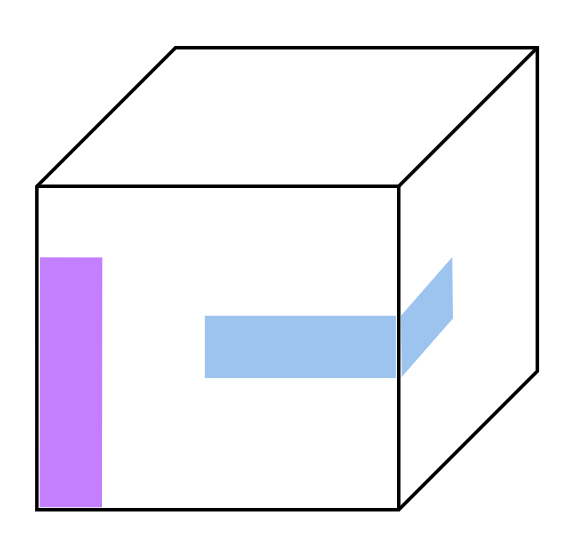
Imagine you have a cube (a box with six square sides). First, cut 16 identical colourful rectangular paper strips of any size you like (choose one size and make all 16 the same). Can you cover the entire outside surface of the cube with these strips, with no gaps and no overlapping? The strips may bend and wrap around edges and corners, but after cutting the 16 strips, you are not allowed to cut them again, and everything must stay on the cube’s surface. Is it possible? Explain why or why not. (For example, two of the strips may look like this: