Problems
We are given a table of size \(n \times n\). \(n-1\) of the cells in the table contain the number \(1\). The remainder contain the number \(0\). We are allowed to carry out the following operation on the table:
1. Pick a cell.
2. Subtract 1 from the number in that cell.
3. Add 1 to every other cell in the same row or column as the chosen cell.
Is it possible, using only this operation, to create a table in which all the cells contain the same number?
Prove that the 13th day of the month is more likely to occur on a Friday than on other days of the week. It is assumed that we live in the Gregorian style calendar.
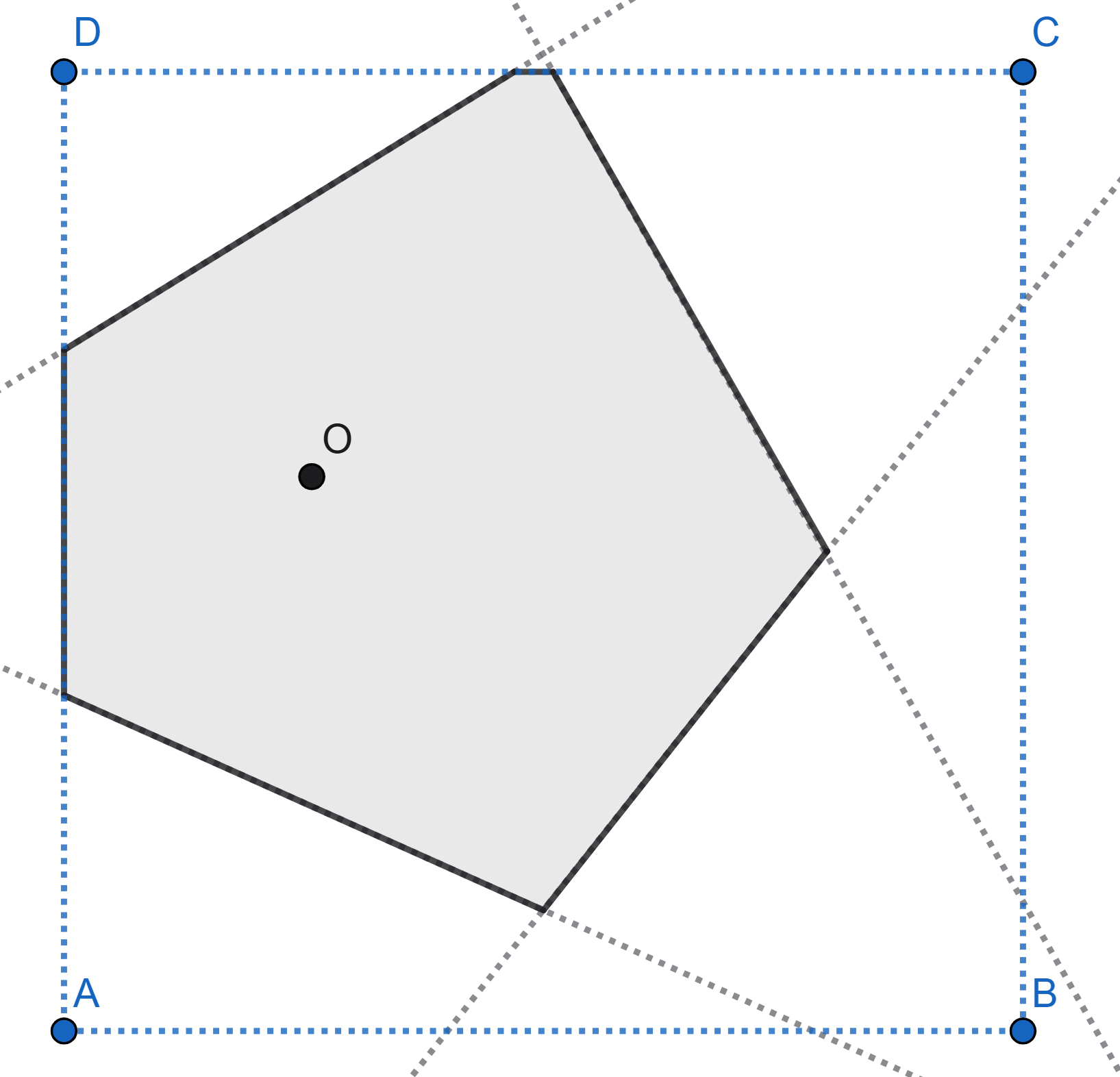
The point \(O\) is randomly chosen on piece of square paper. Then the square is folded in such a way that each vertex is overlaid on the point \(O\). The figure shows one of the possible folding schemes. Find the mathematical expectation of the number of sides of the polygon that appears.
What has a greater value: \(300!\) or \(100^{300}\)?
A numerical sequence is defined by the following conditions: \[a_1 = 1, \quad a_{n+1} = a_n + \lfloor \sqrt{a_n}\rfloor .\]
Prove that among the terms of this sequence there are an infinite number of complete squares.