Problems

Prove that for any positive integer \(n\) the inequality

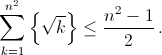
is true.

Find the largest natural number \(n\) which satisfies \(n^{200} <5^{300}\).

Of the four inequalities \(2x > 70\), \(x < 100\), \(4x > 25\) and \(x > 5\), two are true and two are false. Find the value of \(x\) if it is known that it is an integer.

Prove that \(\frac {1}{2} (x^2 + y^2) \geq xy\) for any \(x\) and \(y\).

Prove that for \(x \geq 0\) the inequality is valid: \(2x + \frac {3}{8} \ge \sqrt[4]{x}\).

On a plane, there are 1983 points and a circle of unit radius. Prove that there is a point on the circle, from which the sum of the distances to these points is no less than 1983.

Prove that \(\sqrt{\frac{a^2 + b^2}{2}} \geq \frac{a+b}{2}\).

We are given rational positive numbers \(p, q\) where \(1/p + 1/q = 1\). Prove that for positive \(a\) and \(b\), the following inequality holds: \(ab \leq \frac{a^p}{p} + \frac{b^q}{q}\).

Let \(p\) and \(q\) be positive numbers where \(1 / p + 1 / q = 1\). Prove that \[a_1b_1 + a_2b_2 + \dots + a_nb_n \leq (a_1^p + \dots a_n^p)^{1/p}(b_1^q +\dots + b_n^q)^{1/q}\] The values of the variables are considered positive.

You are mixing four magic potions, and you choose how much of each one to use. Let \(a\), \(b\), \(c\), and \(d\) be the amounts of the four potions you pour in, each chosen between \(0\) and \(1\) liter. The wizard tells you that the magic power of your mix is given by the formula \[a + b + c + d - ab - bc - cd - da.\] What is the largest magic power you can create?