Problems

Cut an arbitrary triangle into 3 parts and out of these pieces construct a rectangle.

Cut the following shape into two equal parts.

Cut the following shape into four equal figures.

Daniel has drawn on a sheet of paper a circle and a dot inside it. Show that he can cut a circle into two parts which can be used to make a circle in which the marked point would be the center.

Is it possible to cut such a hole in \(10\times 10 \,\,cm^2\) piece of paper, though which you can step?

Suppose that a rectangle can be divided into \(13\) equal smaller squares. What could be the side lengths of this rectangle?

Cut the "biscuit" into 16 congruent pieces. The sections are not necessarily rectilinear.

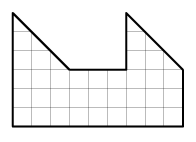
Is it possible to cut this figure, called "camel"

• a) along the grid lines;

• b) not necessarily along the grid lines;

into \(3\) parts, which you can use to build a square?
(We give you several copies to facilitate drawing)

Cut a square into five triangles in such a way that the area of one of these triangles is equal to the sum of the area of other four triangles.

A circular triangle is a triangle in which the sides are arcs of circles. Below is a circular triangle in which the sides are arcs of circles centered at the vertices opposite to the sides.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of the circular triangle.