Problems

Show that for any given even number greater than or equal to \(4\), there is a connected still life with that number of alive cells.

Prove that \(6\) is the maximum possible number of living neighbours a dead cell can have in a still life, and show that this maximum can actually occur.

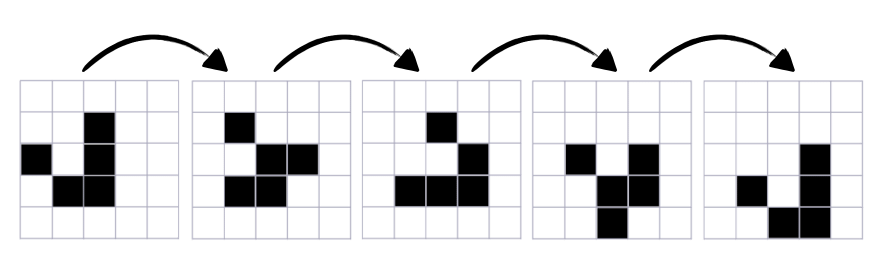
A spaceship is a pattern that, after a fixed number of generations, looks exactly the same as before, but in a different place. For example, the glider is the pattern shown below: it looks the same every \(4\) generations, and each time it has moved one square diagonally. It turns out this is a speed limit in the game! Show that no pattern can move \(2\) or more squares diagonally after \(4\) generations.

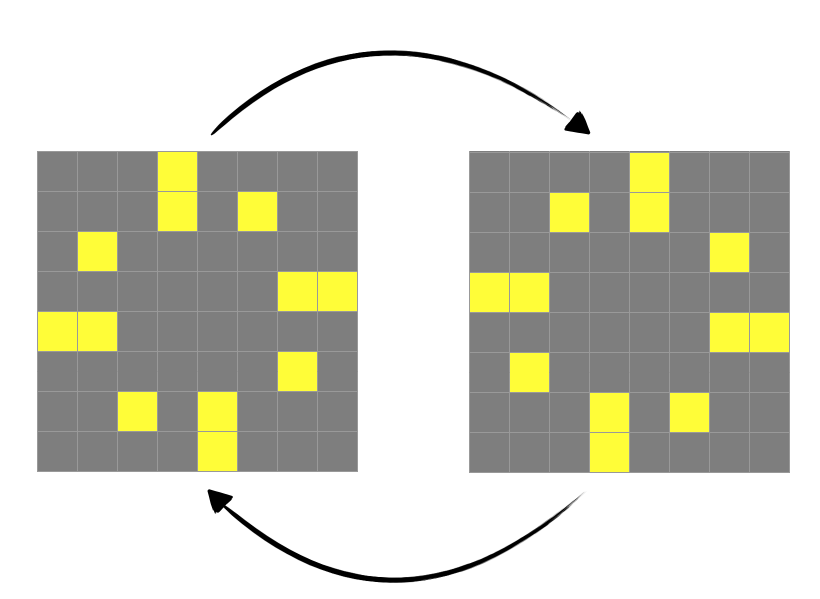
A phoenix is a pattern with the interesting property that all of its alive cells die after each generation, yet the pattern as a whole lives indefinitely. Show that if a phoenix is contained in some rectangle at the start, it can never extend more than once cell past this rectangle (i.e: a phoenix can’t expand forever). Below is a picture of a phoenix with period \(2\):