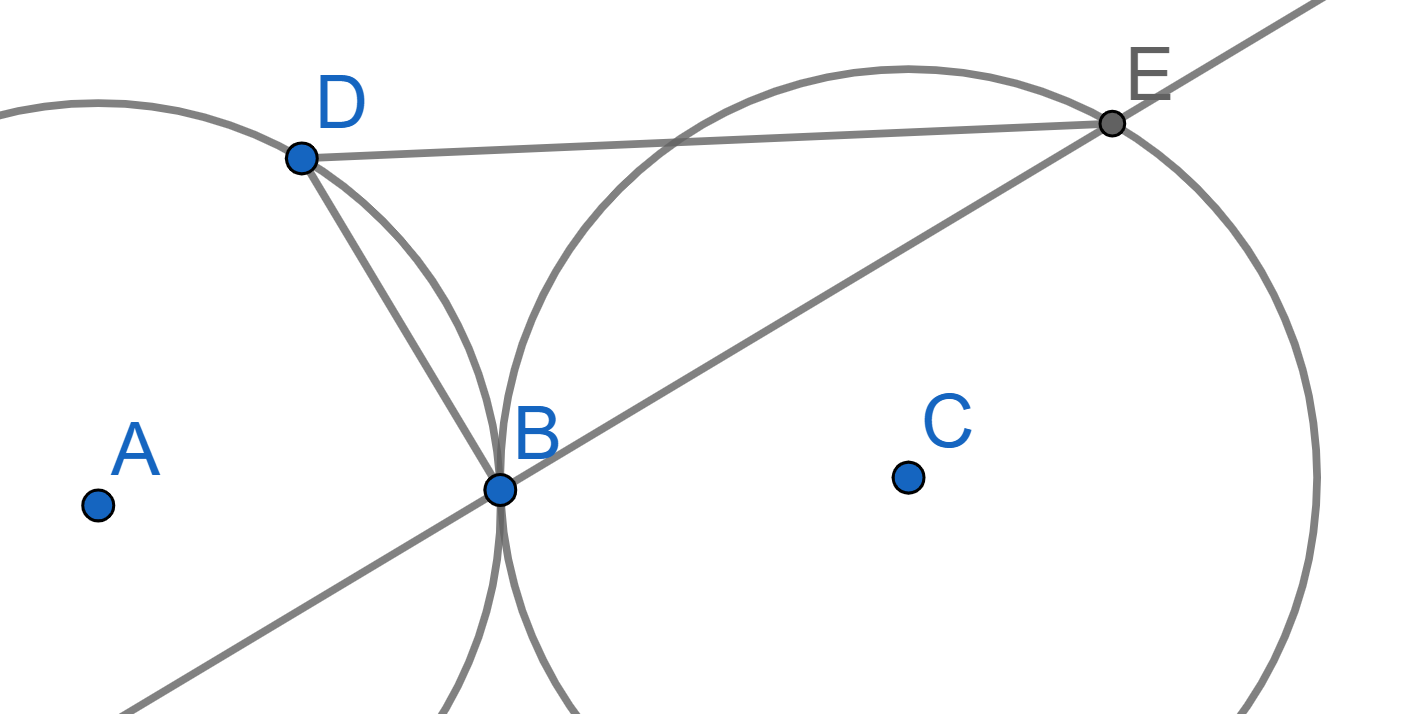
Two circles of radius \(R\) touch at point \(E\). On one of them, point \(B\) is chosen and on the other point \(D\) is chosen. These points have a property of \(\angle BED = 90^{\circ}\). Prove that \(BD = 2R\).
Two circles of radius \(R\) intersect at points \(D\) and \(B\). Let \(F\) and \(G\) be the points of intersection of the middle perpendicular to the segment \(BD\) with these circles lying on one side of the line \(BD\). Prove that \(BD^2 + FG^2 = 4R^2\).