We solve problems

Problems Geometry Plane geometry Area Area of a circle, sector, segment Circles

A maths teacher draws a number of circles on a piece of paper. When she shows this piece of paper to the young mathematician, he claims he can see only five circles. The maths teacher agrees. But when she shows the same piece of paper to another young mathematician, he says that there are exactly eight circles. The teacher confirms that this answer is also correct. How is that possible and how many circles did she originally draw on that piece of paper?

Problem #PRU-100596

Problems Geometry Plane geometry Area Area of a circle, sector, segment Circles

What is the ratio between the red and blue area? All shapes are semicircles.

Problem #PRU-100644

Problems Geometry Plane geometry Circles Triangles Types of triangles Right-angled triangles Pythagorean theorem and its converse

The marked pink segment (tangent to the inner circle) has length $1$ . Find the area of the green annulus.

Problem #PRU-110157

Problems Geometry Plane geometry Plane transformations Similarity Homothetic transformations, rotations of homothetic transformations Circles Connection between the arc length, the angle, and the chord Calculus Derivative Derivative and multiple roots

14–16 5.0

The circles $σ_{1}$ and $σ_{2}$ intersect at points $A$ and $B$ . At the point $A$ to $σ_{1}$ and $σ_{2}$ , respectively, the tangents $l_{1}$ and $l_{2}$ are drawn. The points $T_{1}$ and $T_{2}$ are chosen respectively on the circles $σ_{1}$ and $σ_{2}$ so that the angular measures of the arcs $T_{1} A$ and $A T_{2}$ are equal (the arc value of the circle is considered in the clockwise direction). The tangent $t_{1}$ at the point $T_{1}$ to the circle $σ_{1}$ intersects $l_{2}$ at the point $M_{1}$ . Similarly, the tangent $t_{2}$ at the point $T_{2}$ to the circle $σ_{2}$ intersects $l_{1}$ at the point $M_{2}$ . Prove that the midpoints of the segments $M_{1} M_{2}$ are on the same line, independent of the positions of the points $T_{1}, T_{2}$ .

Problem #PRU-116087

Problems Geometry Plane geometry Triangles Similar triangles Circles Tangent lines and tangent circles Tangent lines to circles

15–16 4.0

Three circles are constructed on a triangle, with the medians of the triangle forming the diameters of the circles. It is known that each pair of circles intersects. Let $C_{1}$ be the point of intersection, further from the vertex $C$ , of the circles constructed from the medians $A M_{1}$ and $B M_{2}$ . Points $A_{1}$ and $B_{1}$ are defined similarly. Prove that the lines $A A_{1}$ , $B B_{1}$ and $C C_{1}$ intersect at the same point.

Problem #PRU-116573

Problems Geometry Plane geometry Circles Diameter, chords, and secants Chords and secants (other) Polygons Regular polygons

15–17 3.0

We create some segments in a regular $n$ -gon by joining endpoints of the $n$ -gon. What’s the maximum number of such segments while ensuring that no two segments are parallel? The segments are allowed to be sides of the $n$ -gon - that is, joining adjacent vertices of the polygon.

Problem #PRU-58094

Problems Geometry Plane geometry Circles Central angle. Arc length and circumference Connection between the arc length, the angle, and the chord Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–15 4.0

Several chords are drawn through a unit circle. Prove that if each diameter intersects with no more than $k$ chords, then the total length of all the chords is less than $π k$ .

Problem #PRU-58097

Problems Geometry Plane geometry Circles Central angle. Arc length and circumference Plane transformations Projection onto a line Orthogonal projection Methods Pigeonhole principle Pigeonhole principle (angles and lengths)

13–16 3.0

Several circles, whose total length of circumferences is 10, are placed inside a square of side 1. Prove that there will always be some straight line that crosses at least four of the circles.

Problem #PRU-78680

Problems Geometry Plane geometry Circles Central angle. Arc length and circumference Methods Mathematical induction Mathematical induction in geometry Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

13–15 3.0

On a circle of radius 1, the point $O$ is marked and from this point, to the right, a notch is marked using a compass of radius $l$ . From the obtained notch $O_{1}$ , a new notch is marked, in the same direction with the same radius and this is process is repeated 1968 times. After this, the circle is cut at all 1968 notches, and we get 1968 arcs. How many different lengths of arcs can this result in?

Problem #WSP-000165

Problems Geometry Plane geometry Circles

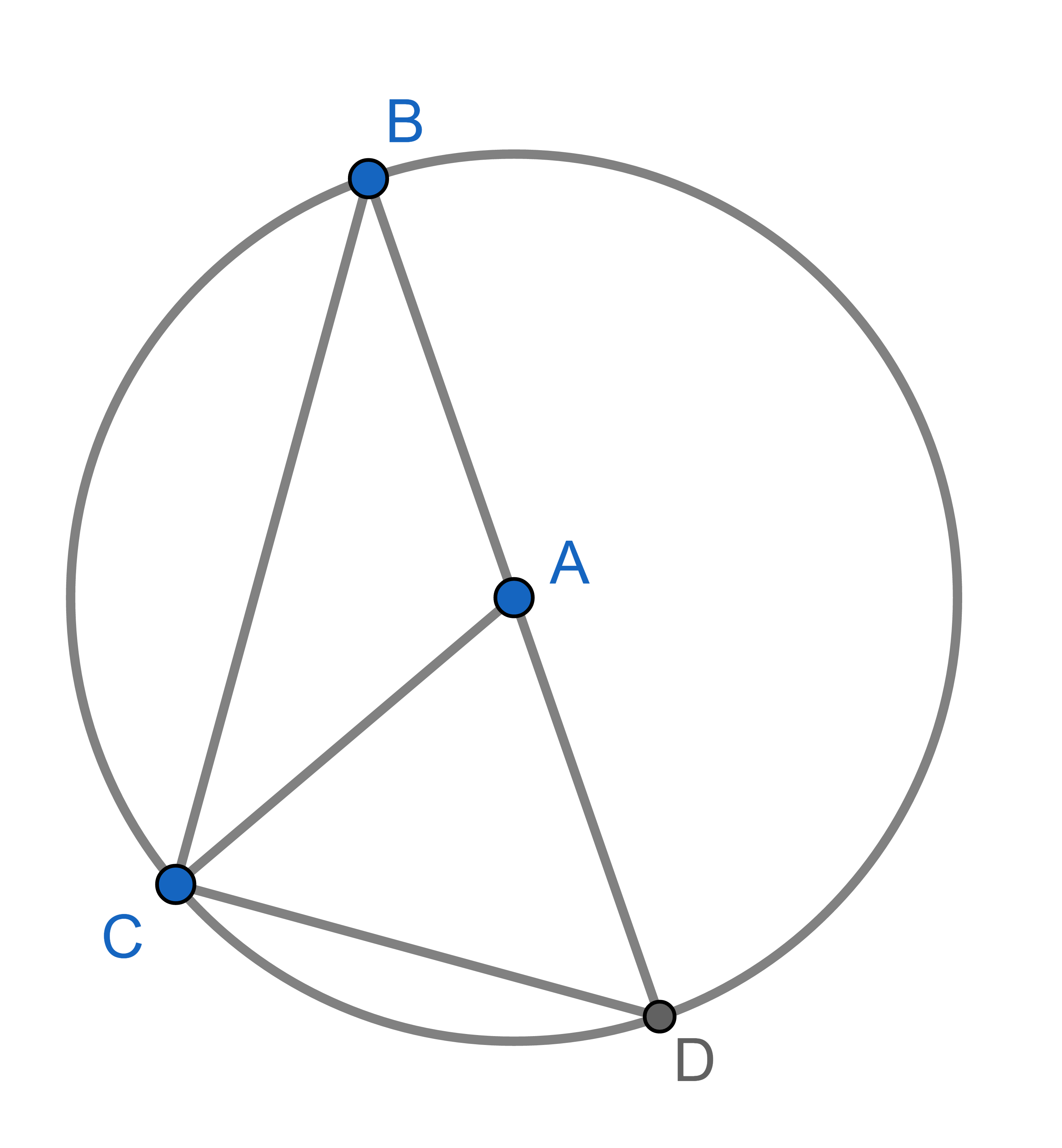
Point $A$ is the centre of a circle and points $B, C, D$ lie on that circle. The segment $B D$ is a diameter of the circle. Show that $∠ C A D = 2 ∠ C B D$ . This is a special case of the inscribed angle theorem.