Problems

A maths teacher draws a number of circles on a piece of paper. When she shows this piece of paper to the young mathematician, he claims he can see only five circles. The maths teacher agrees. But when she shows the same piece of paper to another young mathematician, he says that there are exactly eight circles. The teacher confirms that this answer is also correct. How is that possible and how many circles did she originally draw on that piece of paper?

What is the ratio between the red and blue area? All shapes are semicircles.

The marked pink segment (tangent to the inner circle) has length $1$. Find the area of the green annulus.

The circles ${\sigma }_1$ and ${\sigma }_2$ intersect at points $A$ and $B$. At the point $A$ to ${\sigma }_1$ and ${\sigma }_2$, respectively, the tangents $l_1$ and $l_2$ are drawn. The points $T_1$ and $T_2$ are chosen respectively on the circles ${\sigma }_1$ and ${\sigma }_2$ so that the angular measures of the arcs $T_{1}A$ and $A{T}_2$ are equal (the arc value of the circle is considered in the clockwise direction). The tangent $t_1$ at the point $T_1$ to the circle ${\sigma }_1$ intersects $l_2$ at the point $M_1$. Similarly, the tangent $t_2$ at the point $T_2$ to the circle ${\sigma }_2$ intersects $l_1$ at the point $M_2$. Prove that the midpoints of the segments $M_1{M}_2$ are on the same line, independent of the positions of the points $T_1,T_2$.

Point $A$ is the centre of a circle and points $B,C,D$ lie on that circle. The segment $BD$ is a diameter of the circle. Show that $\mathrm{\angle }CAD=2\mathrm{\angle }CBD$. This is a special case of the inscribed angle theorem.

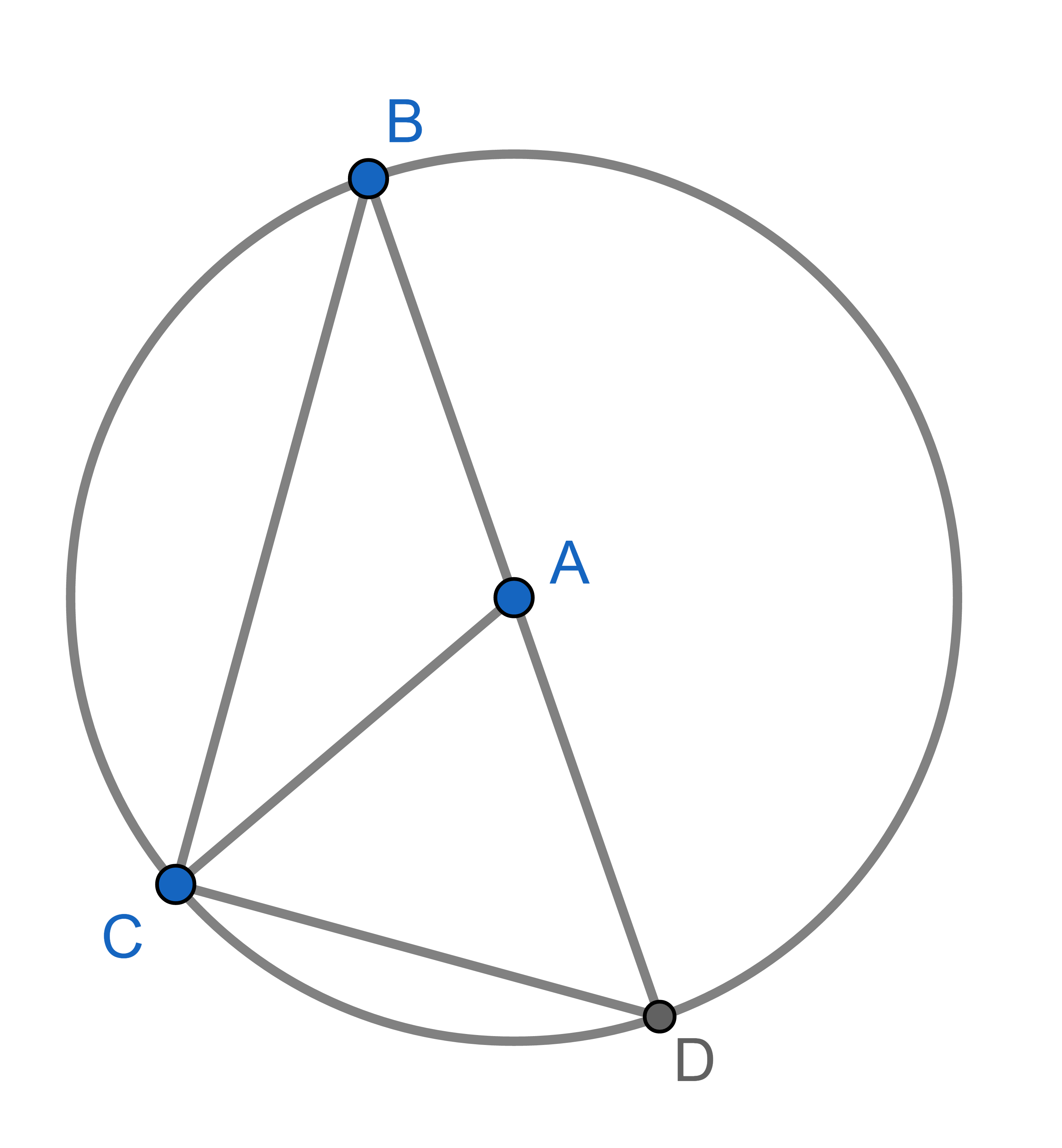
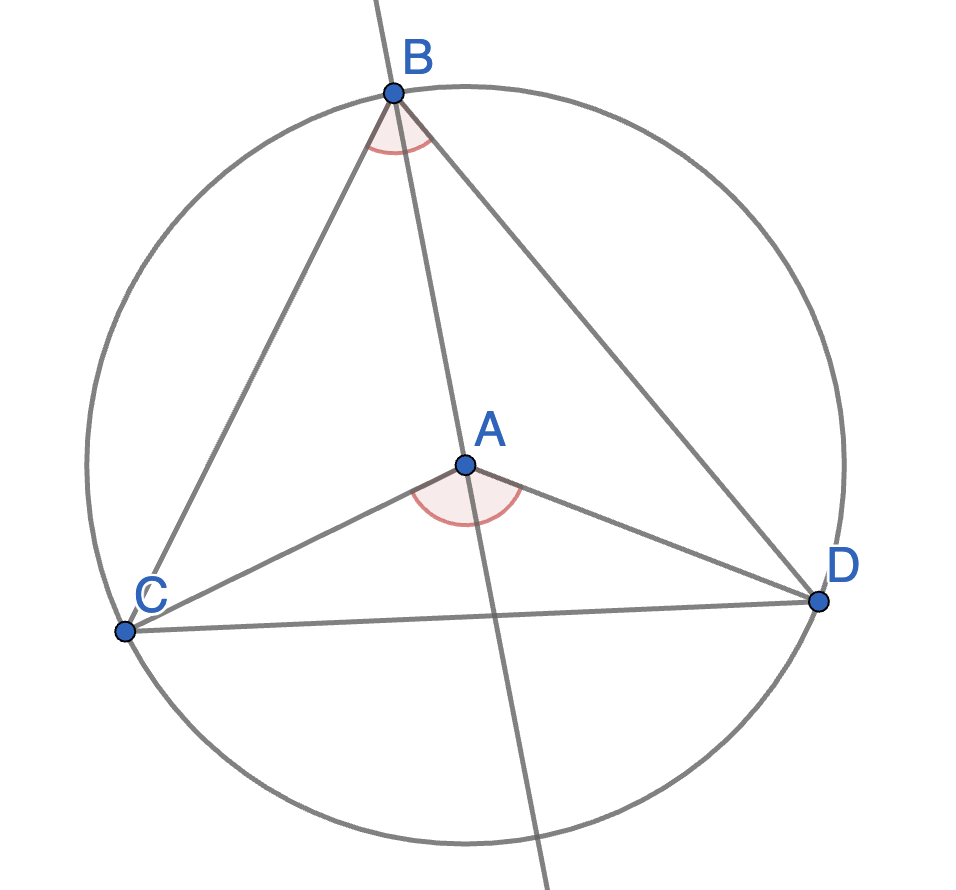
Point $A$ is the centre of a circle and points $B,C,D$ lie on that circle. Show that $\mathrm{\angle }CAD=2\mathrm{\angle }CBD$. This statement is known as the inscribed angle theorem and is used widely in Euclidean geometry.

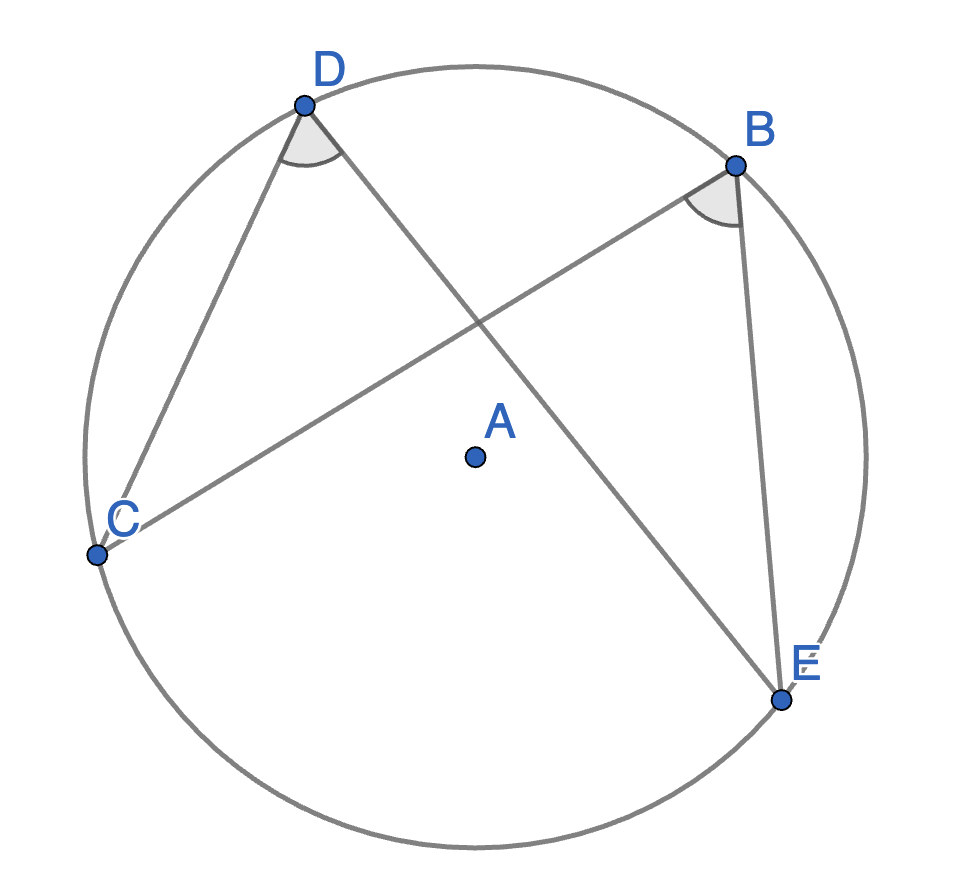
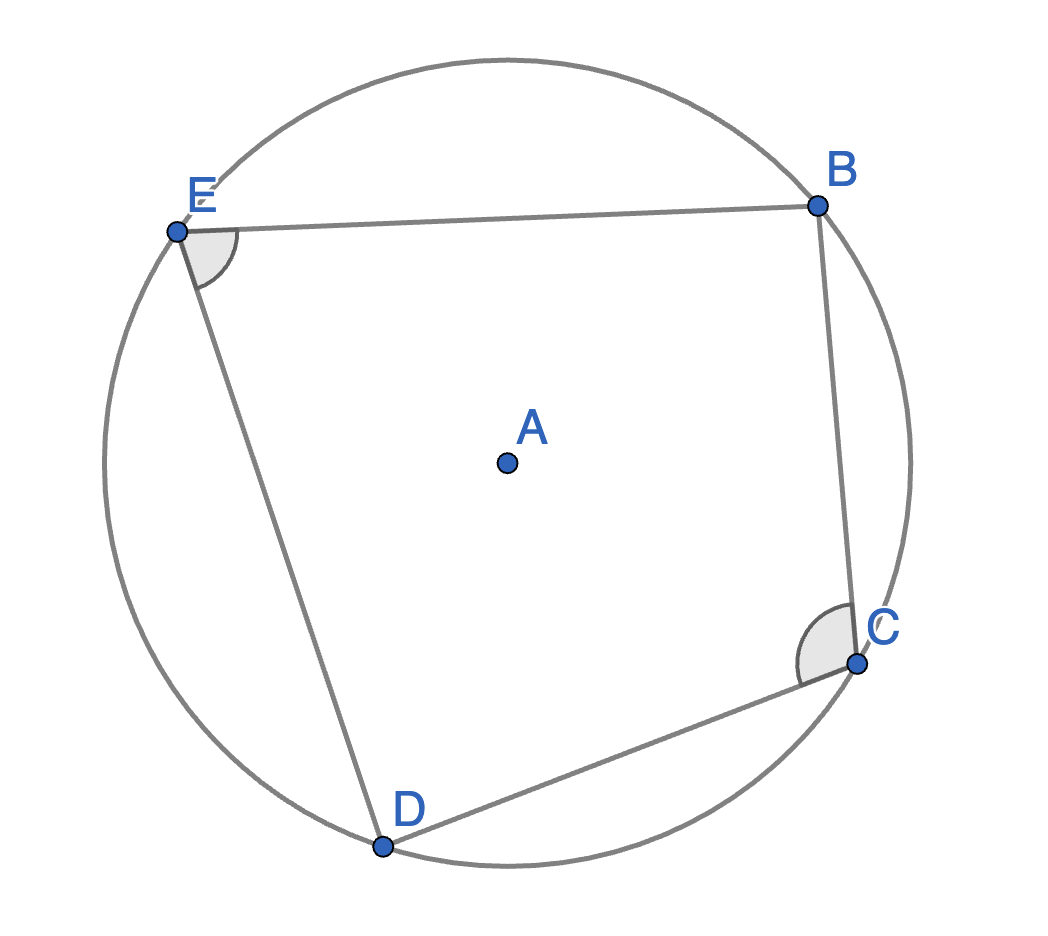
Let $BCDE$ be a quadrilateral inscribed in a circle with centre $A$. Show that angles $\mathrm{\angle }CDE$ and $\mathrm{\angle }CBE$ are equal. Also show that angles $\mathrm{\angle }BCD$ and $\mathrm{\angle }BED$ are equal. This says that all angles at the circumference subtended by the same arc are equal.

Let $BCDE$ be an inscribed quadrilateral. Show that $\mathrm{\angle }BCD+\mathrm{\angle }BED={180}^{\circ }$.

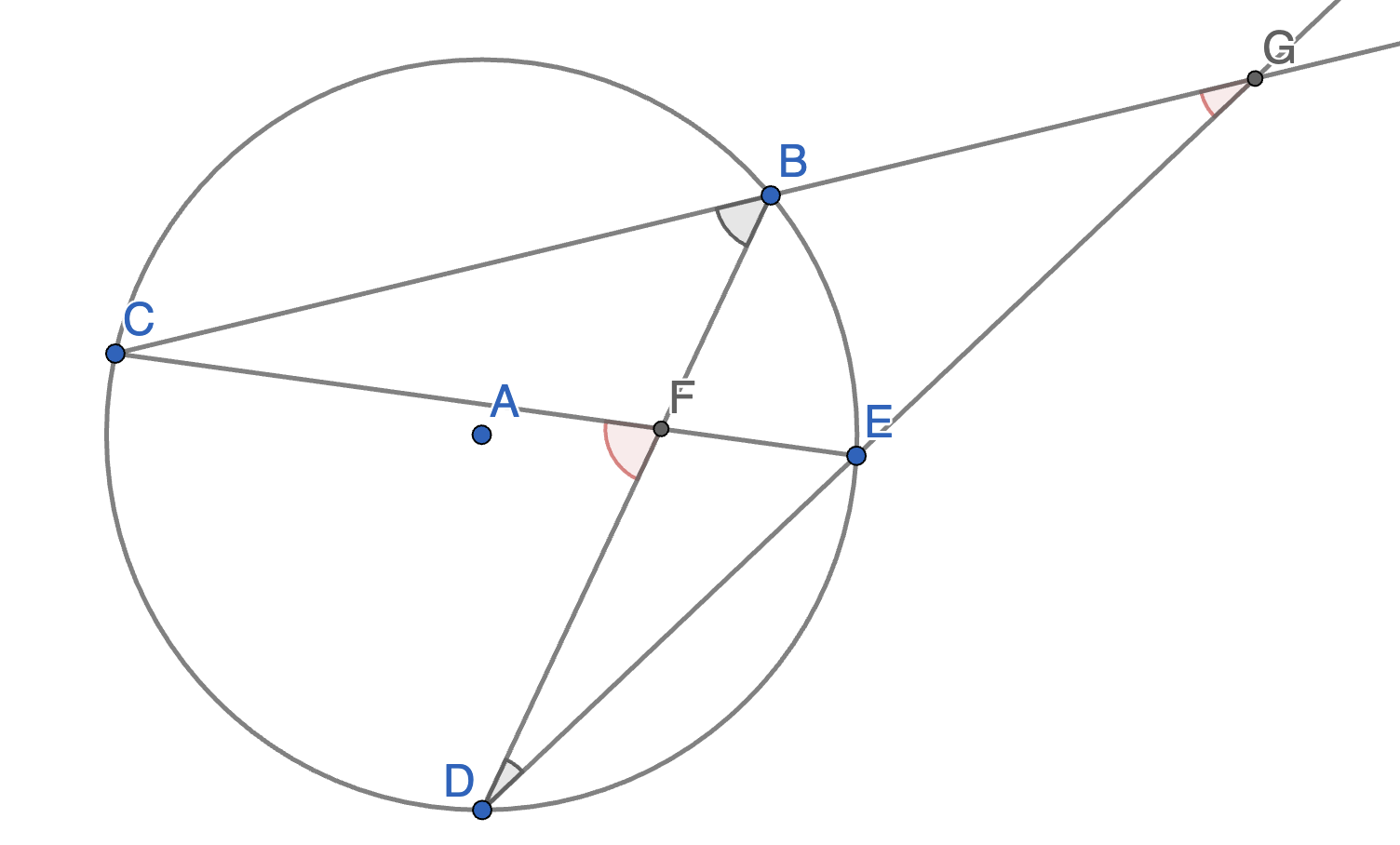
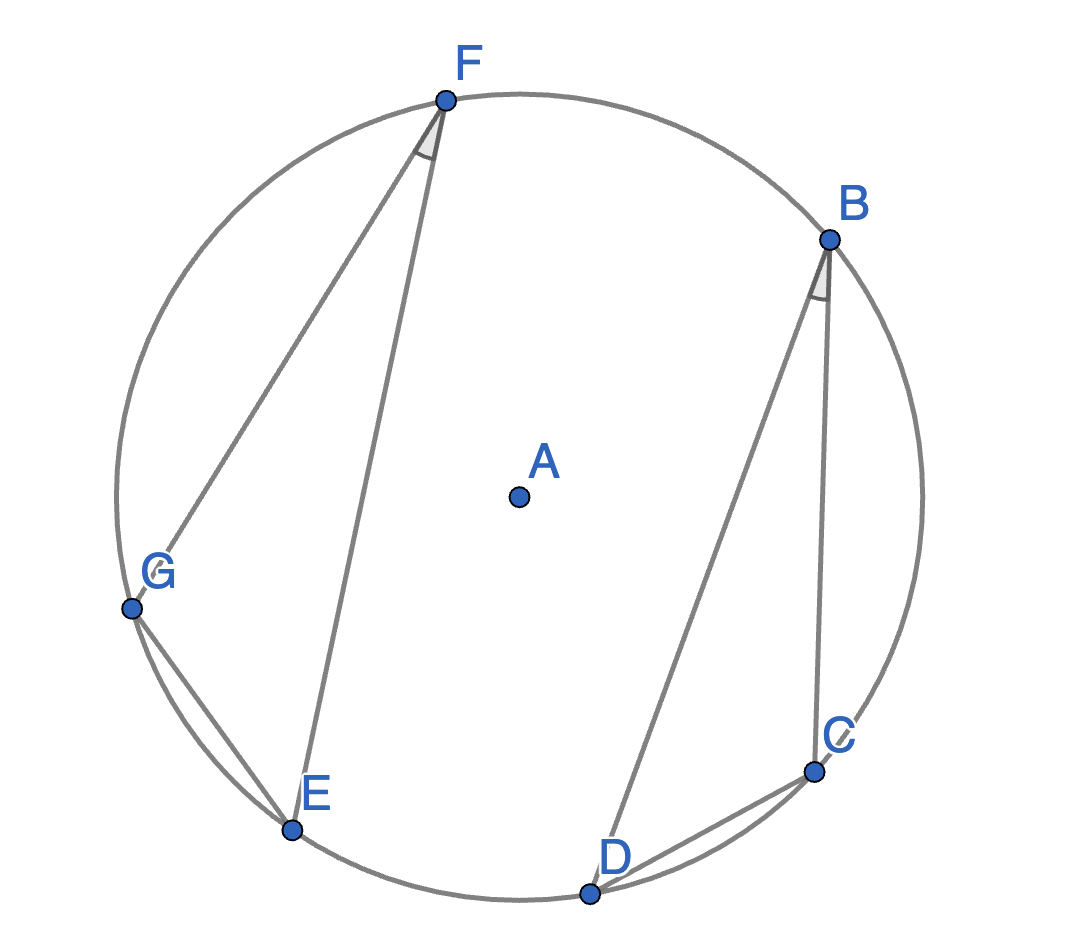
The points $B$,$C$,$D$,$E$,$F$ and $G$ lie on a circle with centre $A$. The angles $\mathrm{\angle }CBD$ and $\mathrm{\angle }EFG$ are equal. Prove that the segments $CD$ and $EG$ have equal lengths.

On the diagram below find the value of the angles $\mathrm{\angle }CFD$ and $\mathrm{\angle }CGD$ in terms of angles $\mathrm{\angle }CBD$ and $\mathrm{\angle }BDE$.