Problems

Let \(x,y\) be nonnegative integers. Determine when \(\text{Nim}(x,y)\) is a losing position and when it is a winning position.

Is \(\text{Nim}(1,2,3)\) a winning position or a losing position?

Is \(\text{Nim}(1,2,4,5,5)\) a winning position or a losing position?

When we write \(137\) in decimal, we mean \(1 \times 10^2 + 3 \times 10 + 7 \times 1\). If we write it instead using powers of \(2\), we have \(137 = 1 \times 2^7 + 0 \times 2^6 + 0 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0\). To tell apart binary representation from decimals, we can use the following notation: \(137 = (10001001)_2\).

What is the number \(273\) in binary? Note that using binary is useful for finding whether a particular Nim game is a winning position or a losing position.

Suppose you have a coffee mug made of stretchy and expandable material. How do you mold it into a donut that has a hole inside?

Take a straight string of finite length. Put the right half on top of the left half to form a hoop, and then pass it (the piece now on top) through the hoop from underneath. Glue the two ends together to form the trefoil knot.

Draw a sequence of pictures to illustrate the formation of the trefoil knot.

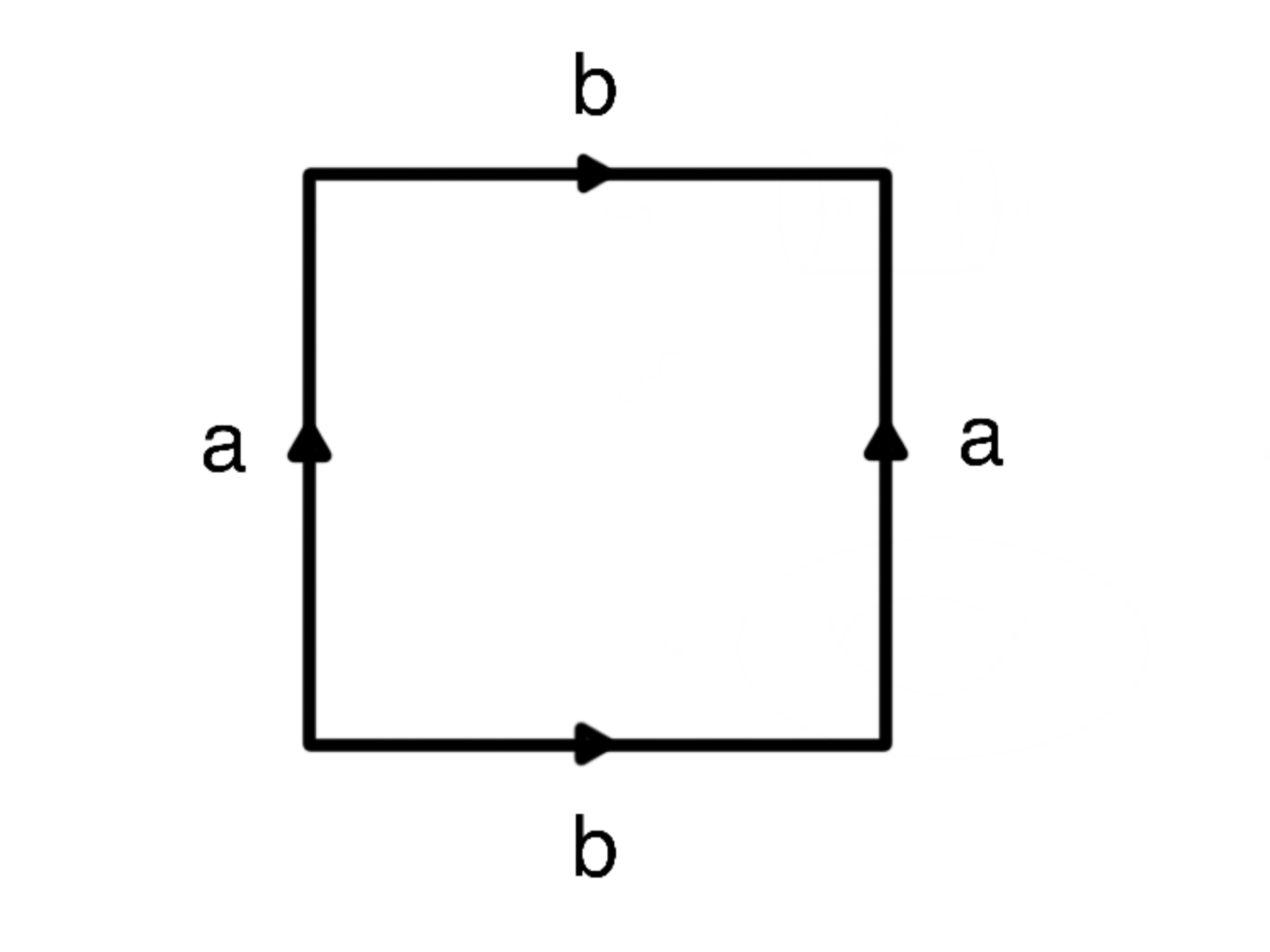
In the picture below, each side is glued in the same direction as its opposite side. Draw a sequence of pictures to show the gluing process and the final shape.

Take a straight string of finite length. Wrap the right half over and then under the left half so that it is pointing to the right again and there is a hoop. Pass the right pointing piece through the hoop from above. Glue the two ends together to form the figure-8 knot.

Draw a sequence of pictures to illustrate the formation of the figure-8 knot, seen below.

Explain why it is possible to have a picture of a figure-8 knot with 100 crossings.

The unknot is the simplest knot, formed by taking a piece of straight string and gluing its two ends together. In reality, there is no knot! Now, which of the following two knots is the unknot?

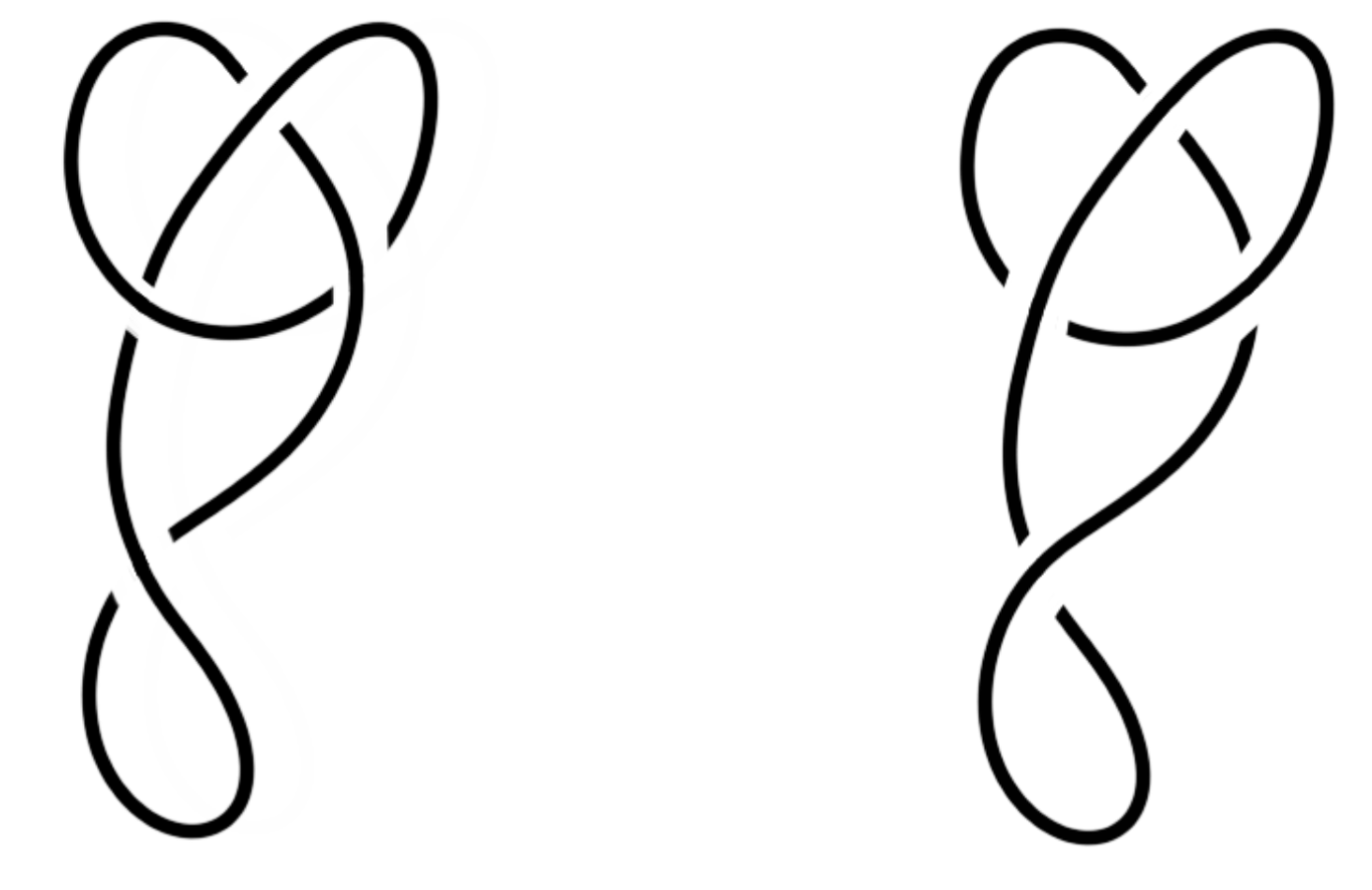
Show that a knot that can be drawn with only one crossing must be the unknot.