Problems
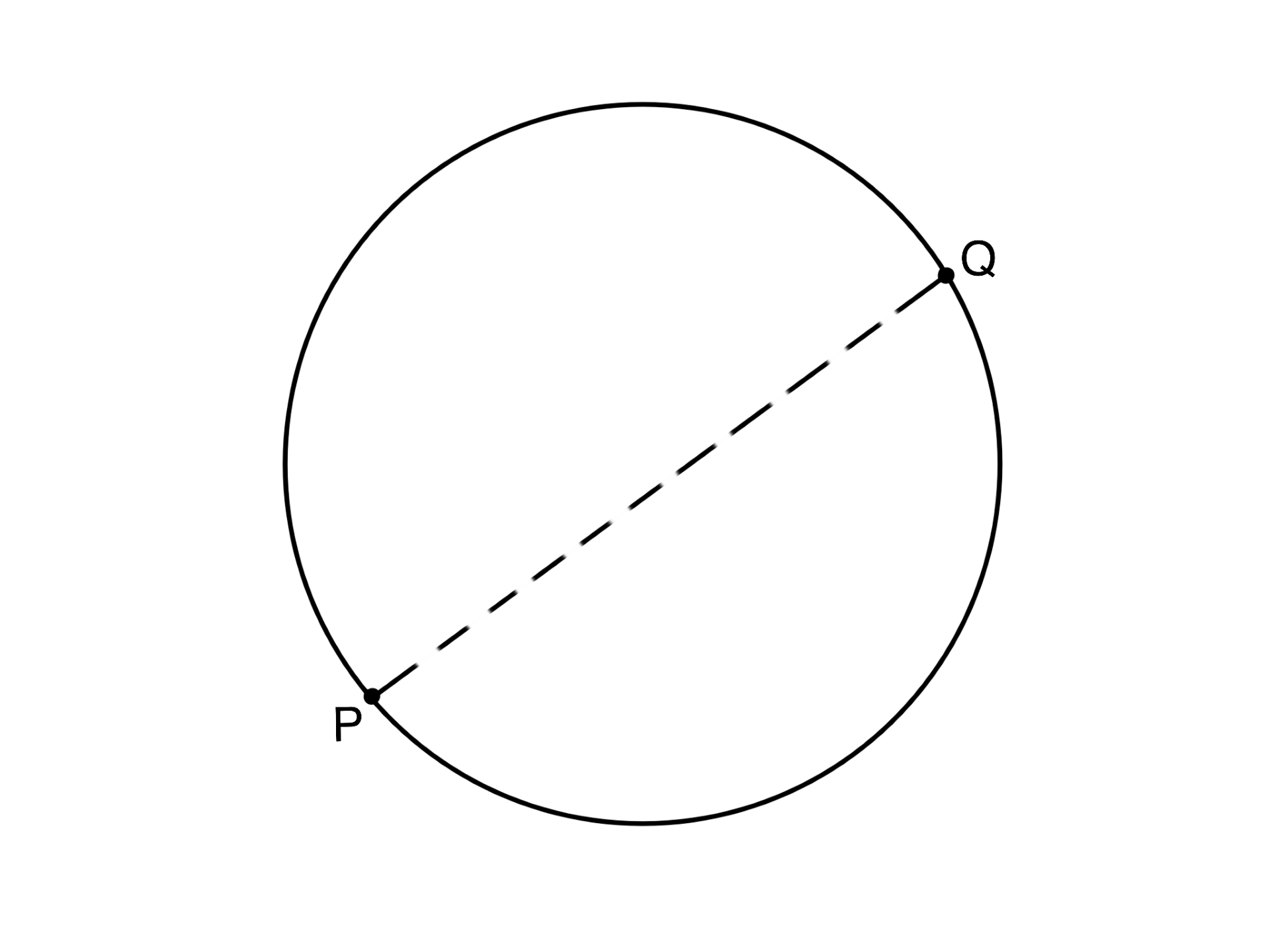
A pair of points on a circle are said to be antipodal if they are on two opposite ends of a common diameter. P and Q in the picture are antipodal points. If we glue every pair of antipodal points on a circle, then what is the resulting shape?
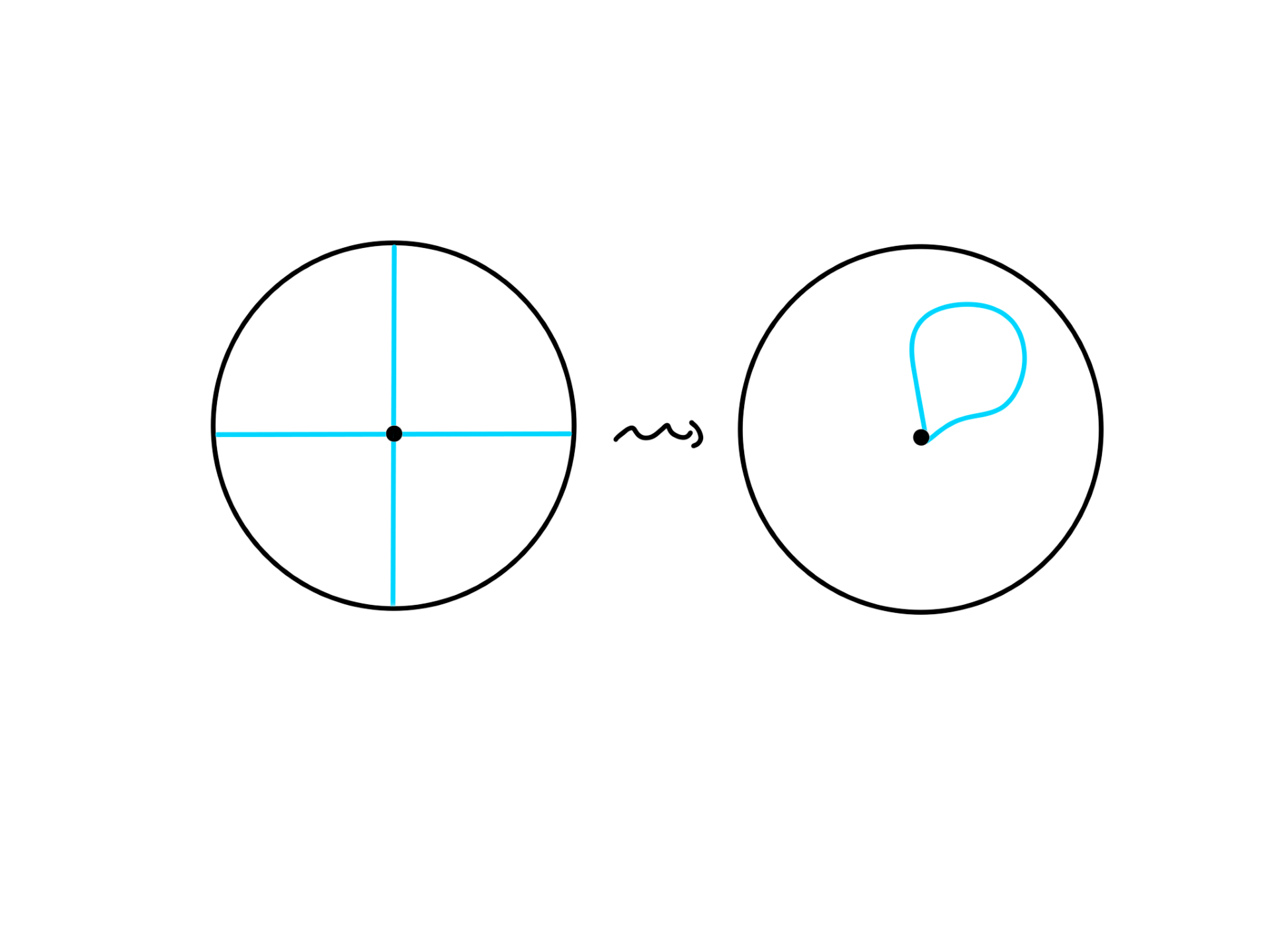
A surface P is created by gluing every pair of antipodal points of a disc (a circle with inside filled in). We represent P on the plane by a disc in the following picture and bear in mind that the antipodal points are glued.
Explain why the two diameters in the pictures are in fact two circles on P and how to stretch it so that it becomes a single loop not touching any of the glued points.
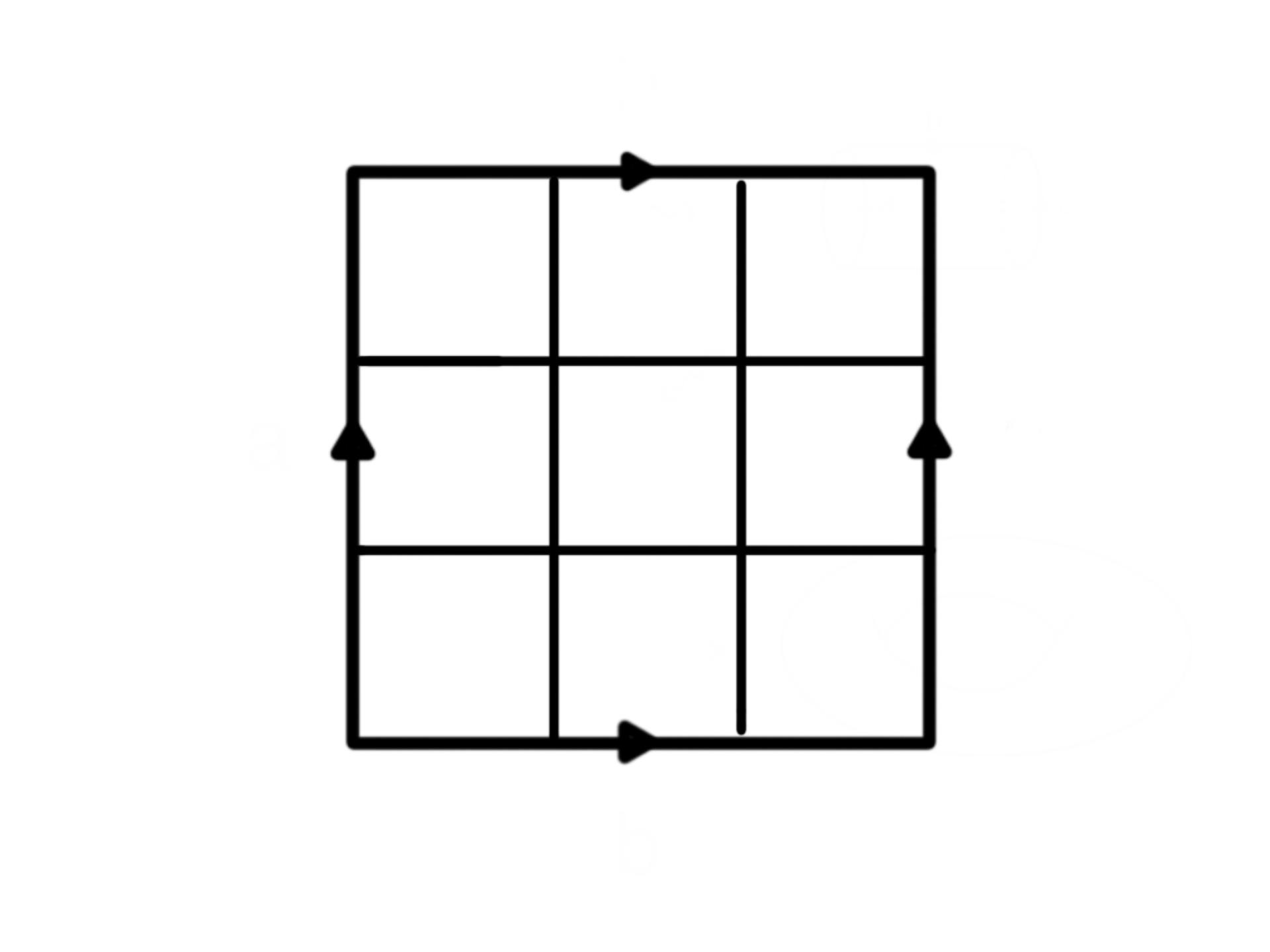
It is possible to play tic-tac-toe on a torus: gluing the sides means that the bottom row is above the top row and the right most column is also to the left of the left most column. Is one of the players guaranteed to win if they play all the right moves?
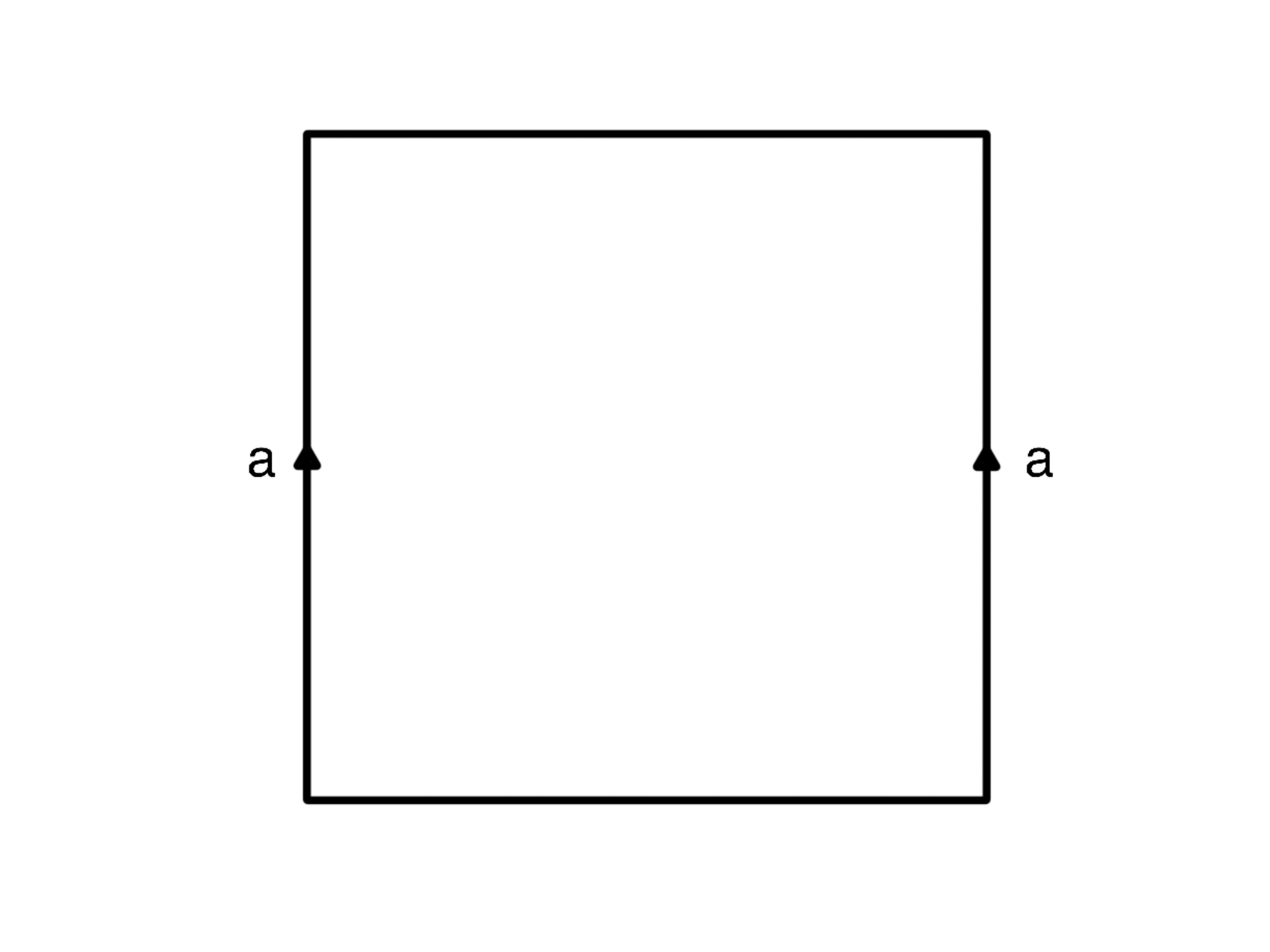
Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the same direction as in the picture.
What is logically the opposite of the statement “every \(n\) is odd or \(p<q\)"?
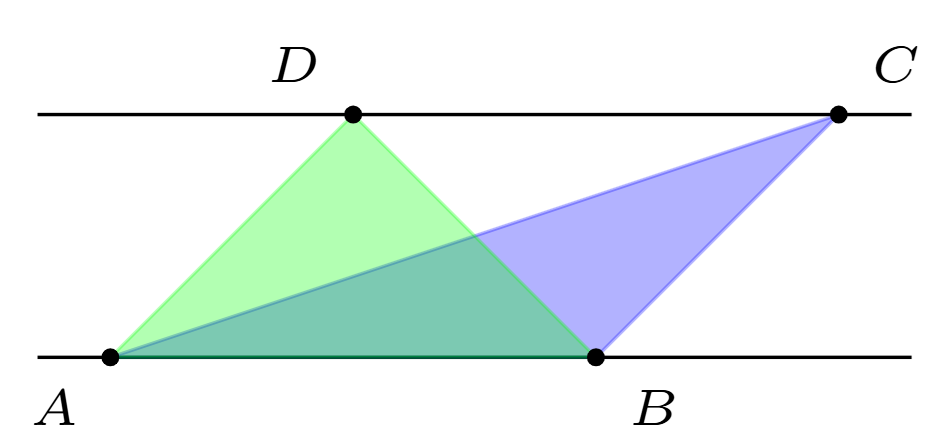
There is a pair of parallel lines. The point \(A\) and \(B\) lie on one of the lines. The point \(C\) and \(D\) lies on the other line. We can form triangles \(\triangle ABC\) and \(\triangle ABD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
What’s the sum of the Fibonacci numbers \(F_0+F_1+F_2+...+F_n\)?
What’s the sum \(\frac{F_2}{F_1}+\frac{F_4}{F_2}+\frac{F_6}{F_3}+...+\frac{F_{18}}{F_9}+\frac{F_{20}}{F_{10}}\)?