Problems
Sage thought of the sum of some three natural numbers, and the Patricia thought about their product.
“If I knew,” said Sage, “that your number is greater than mine, then I would immediately name the three numbers that are needed.”
“My number is smaller than yours,” Patricia answered, “and the numbers you want are ..., ... and ....”
What numbers did Patricia name?
Ben noticed that all 25 of his classmates have a different number of friends in this class. How many friends does Ben have?
Initially, a natural number \(A\) is written on a board. You are allowed to add to it one of its divisors, distinct from itself and one. With the resulting number you are permitted to perform a similar operation, and so on.
Prove that from the number \(A = 4\) one can, with the help of such operations, come to any given in advance composite number.
A student did not notice the multiplication sign between two three-digit numbers and wrote one six-digit number. The result was three times greater.
Find these numbers.
There is a chocolate bar with five longitudinal and eight transverse grooves, along which it can be broken (in total into \(9 * 6 = 54\) squares). Two players take part, in turns. A player in his turn breaks off the chocolate bar a strip of width 1 and eats it. Another player who plays in his turn does the same with the part that is left, etc. The one who breaks a strip of width 2 into two strips of width 1 eats one of them, and the other is eaten by his partner. Prove that the first player can act in such a way that he will get at least 6 more chocolate squares than the second player.
During the ball every young man danced the waltz with a girl, who was either more beautiful than the one he danced with during the previous dance, or more intelligent, but most of the men (at least 80%) – with a girl who was at the same time more beautiful and more intelligent. Could this happen? (There was an equal number of boys and girls at the ball.)
A \(1 \times 10\) strip is divided into unit squares. The numbers \(1, 2, \dots , 10\) are written into squares. First, the number 1 is written in one square, then the number 2 is written into one of the neighboring squares, then the number 3 is written into one of the neighboring squares of those already occupied, and so on (the choice of the first square is made arbitrarily and the choice of the neighbor at each step). In how many ways can this be done?
Imagine an infinitely large sheet of paper with a square drawn on it. Somewhere on the paper, a point \(P\) is marked with ink that is invisible to you. However, a friend with a special pair of glasses can see the point.
We are allowed to draw straight lines on the paper, and for each line, our friend will tell us on which side of the line the point \(P\) is. (If \(P\) is exactly on the line, they will say so.) For example, on this picture, our friend would say that the point \(P\) is above the line we’ve drawn:
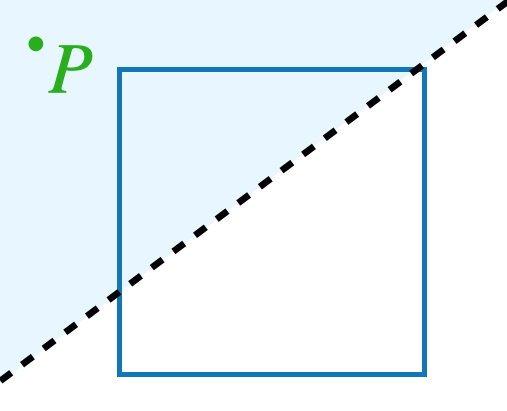
What is the smallest number of such questions that are needed in order to be certain whether \(P\) lies inside the square? Explain why it cannot be done in less questions then you are suggesting.
Two play tic-tac-toe on a \(10 \times 10\) board according to the following rules. First they fill the whole board with noughts and crosses, putting them in turn (the first player puts crosses, their partner – noughts). Then two numbers are counted: \(K\) is the number of five consecutively standing crosses and \(H\) is the number of five consecutively standing zeros. (Five, standing horizontally, vertically and parallel to the diagonal are counted, if there are six crosses in a row, this gives two fives, if there are seven, then three, etc.). The number \(K-H\) is considered to be the winnings of the first player (the losses of the second).
a) Does the first player have a winning strategy?
b) Does the first player have a non-losing strategy?
Initially, on each cell of a \(1 \times n\) board a checker is placed. The first move allows you to move any checker onto an adjacent cell (one of the two, if the checker is not on the edge), so that a column of two pieces is formed. Then one can move each column in any direction by as many cells as there are checkers in it (within the board); if the column is on a non-empty cell, it is placed on a column standing there and unites with it. Prove that in \(n - 1\) moves you can collect all of the checkers on one square.