Problems

Is it possible to cut this figure, called "camel"

• a) along the grid lines;

• b) not necessarily along the grid lines;

into \(3\) parts, which you can use to build a square?
(We give you several copies to facilitate drawing)

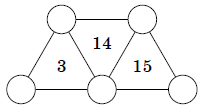
Michael used different numbers \(\{0,1,2,3,4,5,6,7,8,9\}\) to put in the circles in the picture below, without using any one of them twice. Inside each triangle he wrote down either the sum or the product of the numbers at its vertices. Then he erased the numbers in the circles. Which numbers need to be written in circles so that the condition is satisfied?

Find all solutions to the puzzle \(\textrm{AC}\times\textrm{CC}\times\textrm{K} = 2002.\) Different letters correspond to different digits, identical letters correspond to identical digits. Find all solutions.

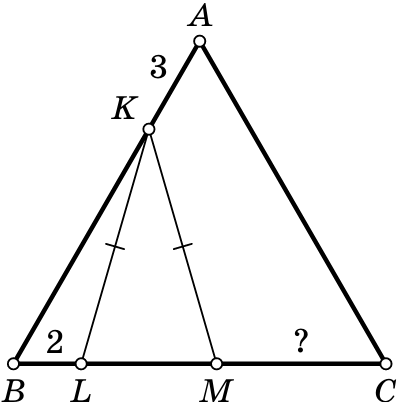
The triangle \(ABC\) is equilateral. The point \(K\) is chosen on the side \(AB\) and points \(L\) and \(M\) are on the side \(BC\) in such a way that \(L\) lies on the segment \(BM\). We have the following properties: \(KL = KM,\) \(BL = 2,\, AK = 3.\) Find the length of \(CM\).

• We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.

• It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.

We prove the other two assertions from the description:

• The sum of all internal angles of a triangle is also \(180^{\circ}\).

• In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).

Find all solutions of the puzzle \(HE \times HE = SHE\). Different letters stand for different digits, and the same letters stand for the same digit.

Frodo ventures into a thick fog where he is to meet his three companions: Sam, Merry, and Pippin. He can tell they are standing in a row, in front of him – one on the left, one in the middle, and one on the right – but he cannot see who is who. To help, he asks each of them to speak.

Remember: Sam always lies, Merry always tells the truth, and Pippin sometimes lies and sometimes tells the truth.

Here is what Frodo hears:

• The one on Frodo’s left says: “Merry is next to me.”

• The one on Frodo’s right says: “The person who just spoke is Pippin.”

• The one in the middle says: “On my left is Sam.”

Can you work out who is standing on Frodo’s left, in the middle, and on the right?

Using areas of squares and rectangles, show that for any positive real numbers \(a\) and \(b\), \((a+b)^2 = a^2+2ab+b^2\).
The identity above is true for any real numbers, not necessarily positive, in fact in order to prove it the usual way one only needs to remember that multiplication is commutative and the distributive property of addition and multiplication:

• \(a\times b = b\times a\);

• \((a+b)\times c = a\times c + b\times c\).