Problems
Cut a square into five triangles in such a way that the area of one of these triangles is equal to the sum of the area of other four triangles.
A circular triangle is a triangle in which the sides are arcs of
circles. Below is a circular triangle in which the sides are arcs of
circles centered at the vertices opposite to the sides.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of the circular triangle.
In a box there are \(20\) cards of different colours: some red, some blue and some yellow. Yellow cards outnumber red ones and there are six times as many yellow cards as blue cards. We draw some cards from the box without looking. What is the minimum number we need to draw to guarantee a red card among them?
There are two piles of rocks, \(10\) rocks in each pile. Fred and George play a game, taking the rocks away. They are allowed to take any number of rocks only from one pile per turn. The one who has nothing to take loses. If Fred starts, who has the winning strategy?
A group of \(15\) elves decided to pay a visit to their relatives in a distant village. They have a horse carriage that fits only \(5\) elves. In how many ways can they assemble the ambassador team, if at least one person in the team needs to be able to operate the carriage, and only \(5\) elves in the group can do that?
There are \(5\) pirates and they want to share \(8\) identical gold coins. In how many ways can they do it if each pirate has to get at least one coin?
Is \(100\times 99 \times ...\times 2\) divisible by \(2^{100}\)?
It is known that \(a + b + c = 5\) and \(ab + bc + ac = 5\). What are the possible values of \(a^2 + b^2 + c^2\)?
Prove the magic trick for the number \(1089
= 33^2\): if you take any \(3\)-digit number \(\overline{abc}\) with digits coming in
strictly descending order and subtract from it the number obtained by
reversing the digits of the original number \(\overline{abc} - \overline{cba}\) you get
another \(3\)-digit number, call it
\(\overline{xyz}\). Then, no matter
which number you started with, the sum \(\overline{xyz} + \overline{zyx} =
1089\).
Recall that a number \(\overline{abc}\)
is divisible by \(11\) if and only if
\(a-b+c\) also is.
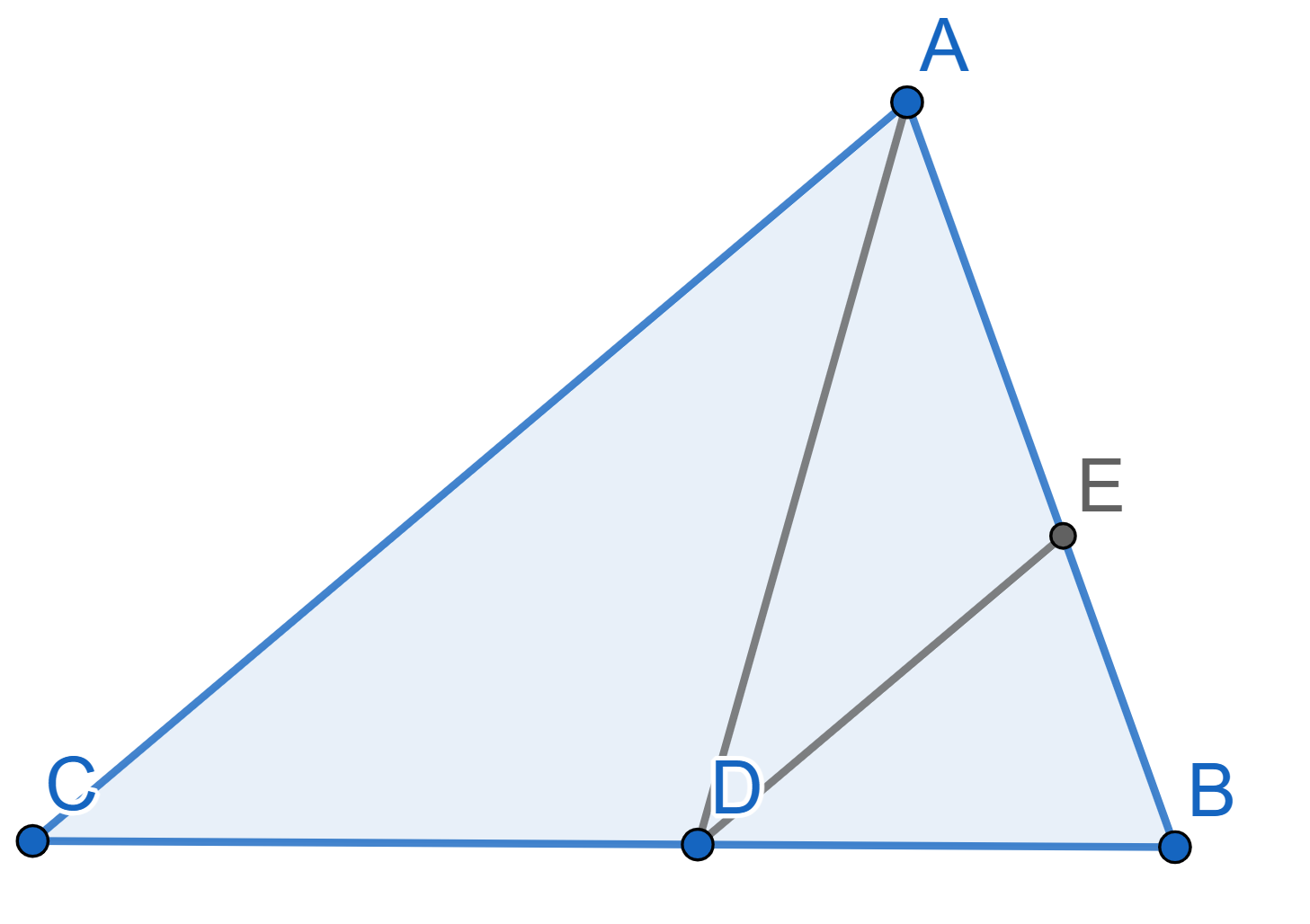
On the diagram below \(AD\) is the
bisector of the triangle \(ABC\). The
point \(E\) lies on the side \(AB\), with \(AE =
ED\). Prove that the lines \(AC\) and \(DE\) are parallel.