Problems
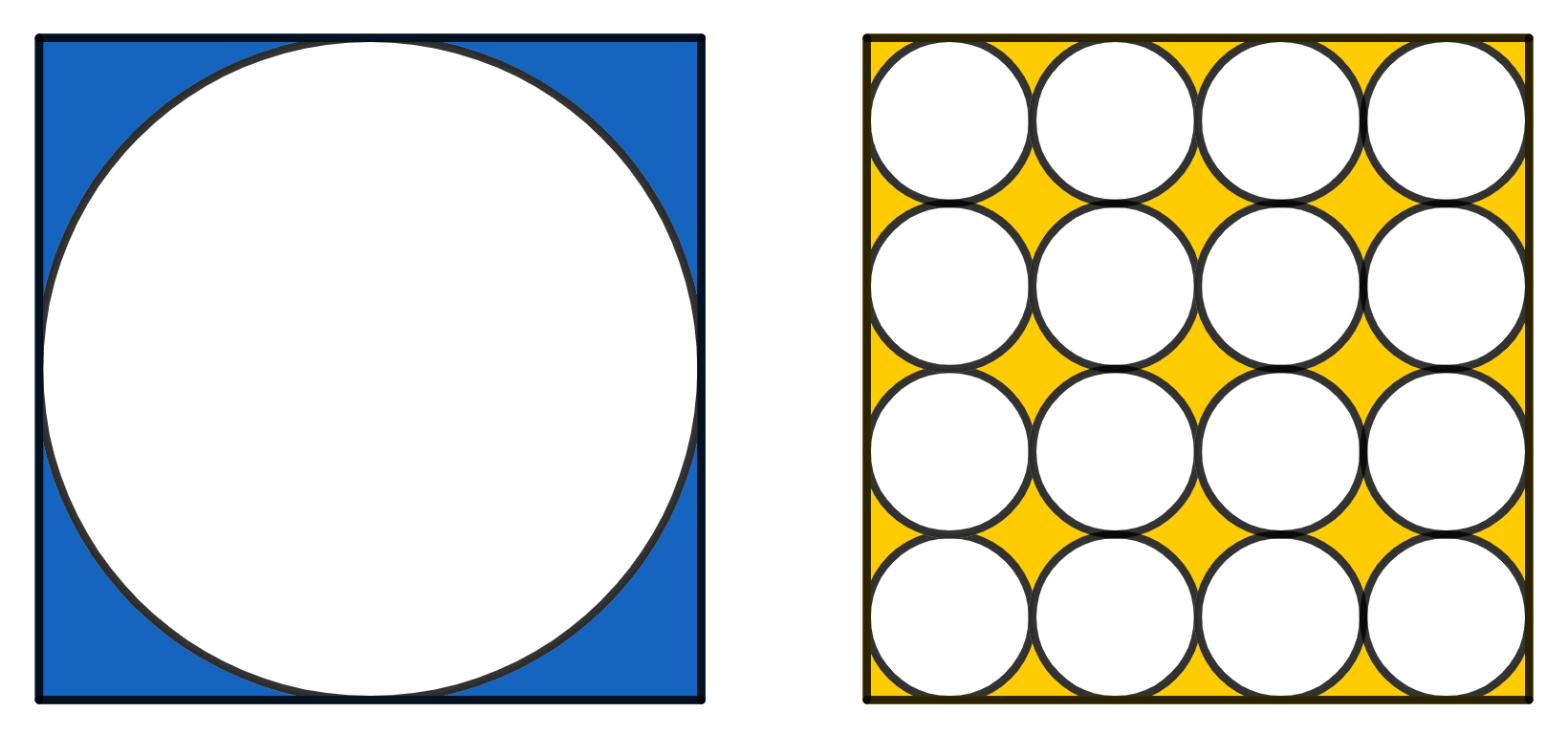
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?
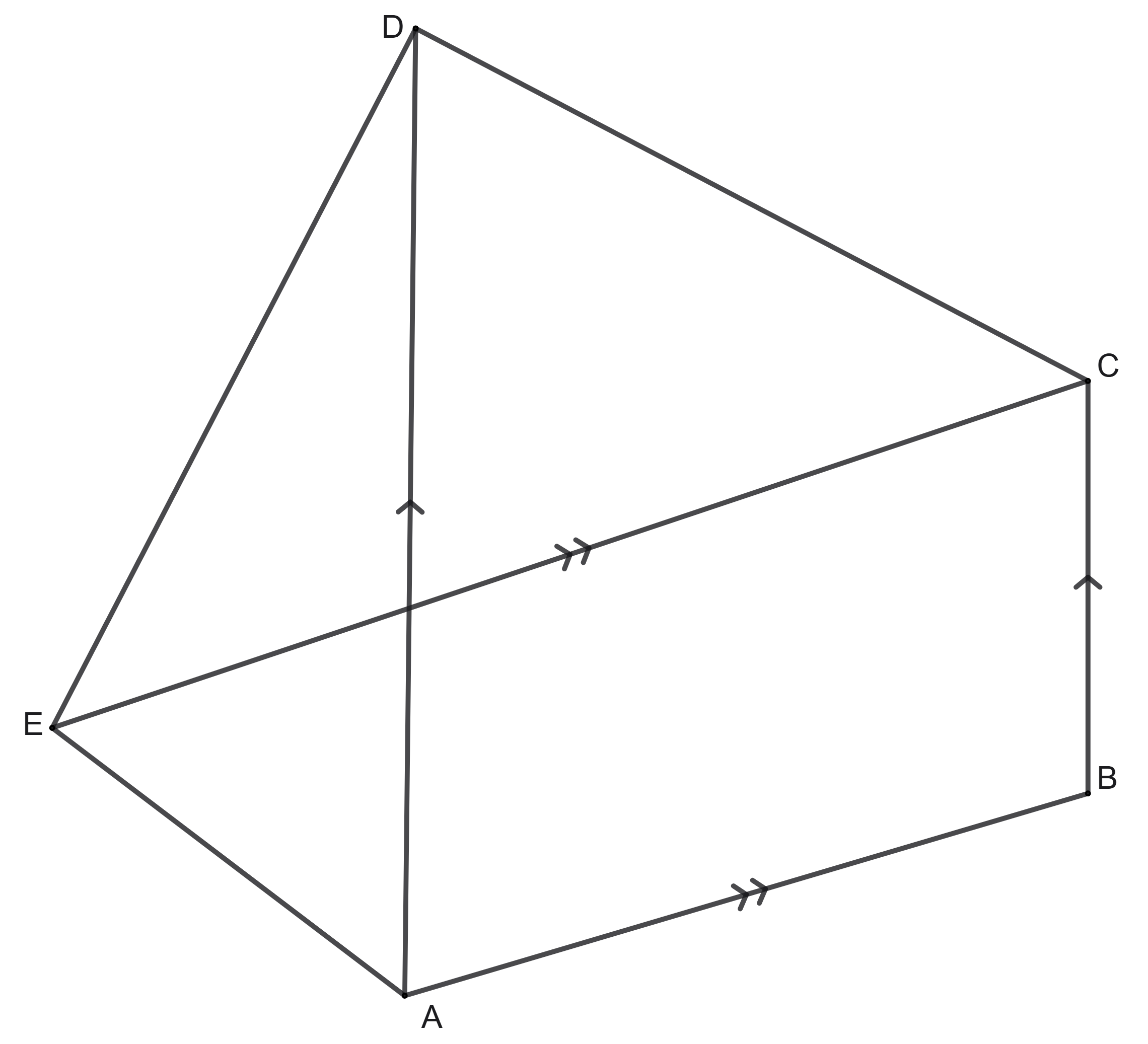
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.
Prove that, for any integer \(n\), among the numbers \(n, n + 1, n + 2, \dots , n + 9\) there is at least one number that is mutually prime with the other nine numbers.
How can you arrange the numbers \(5/177\), \(51/19\) and \(95/9\) and the arithmetical operators “\(+\)”, “\(-\)”, “\(\times\)” and “\(\div\)” such that the result is equal to 2006? Note: you can use the given numbers and operators more than once.
There are 13 weights, each weighing an integer number of grams. It is known that any 12 of them can be divided into two cups of weights, six weights on each one, which will come to equilibrium. Prove that all the weights have the same weight.
The segment \(OA\) is given. From the end of the segment \(A\) there are 5 segments \(AB_1, AB_2, AB_3, AB_4, AB_5\). From each point \(B_i\) there can be five more new segments or not a single new segment, etc. Can the number of free ends of the constructed segments be 1001? By the free end of a segment we mean a point belonging to only one segment (except point \(O\)).
There is a system of equations \[\begin{aligned} * x + * y + * z &= 0,\\ * x + * y + * z &= 0,\\ * x + * y + * z &= 0. \end{aligned}\] Two people alternately enter a number instead of a star. Prove that the player that goes first can always ensure that the system has a non-zero solution.
There are two sets of numbers made up of 1s and \(-1\)s, and in each there are 2022 numbers. Prove that in some number of steps it is possible to turn the first set into the second one if for each step you are allowed to simultaneously change the sign of any 11 numbers of the starting set. (Two sets are considered the same if they have the same numbers in the same places.)
Note that if you turn over a sheet on which numbers are written, then the digits 0, 1, 8 will not change and the digits 6 and 9 will switch places, whilst the others will lose their meaning. How many nine-digit numbers exist that do not change when a sheet is turned over?
Two people play a game with the following rules: one of them guesses a set of integers \((x_1, x_2, \dots , x_n)\) which are single-valued digits and can be either positive or negative. The second person is allowed to ask what is the sum \(a_1x_1 + \dots + a_nx_n\), where \((a_1, \dots ,a_n)\) is any set. What is the smallest number of questions for which the guesser recognizes the intended set?