Problems
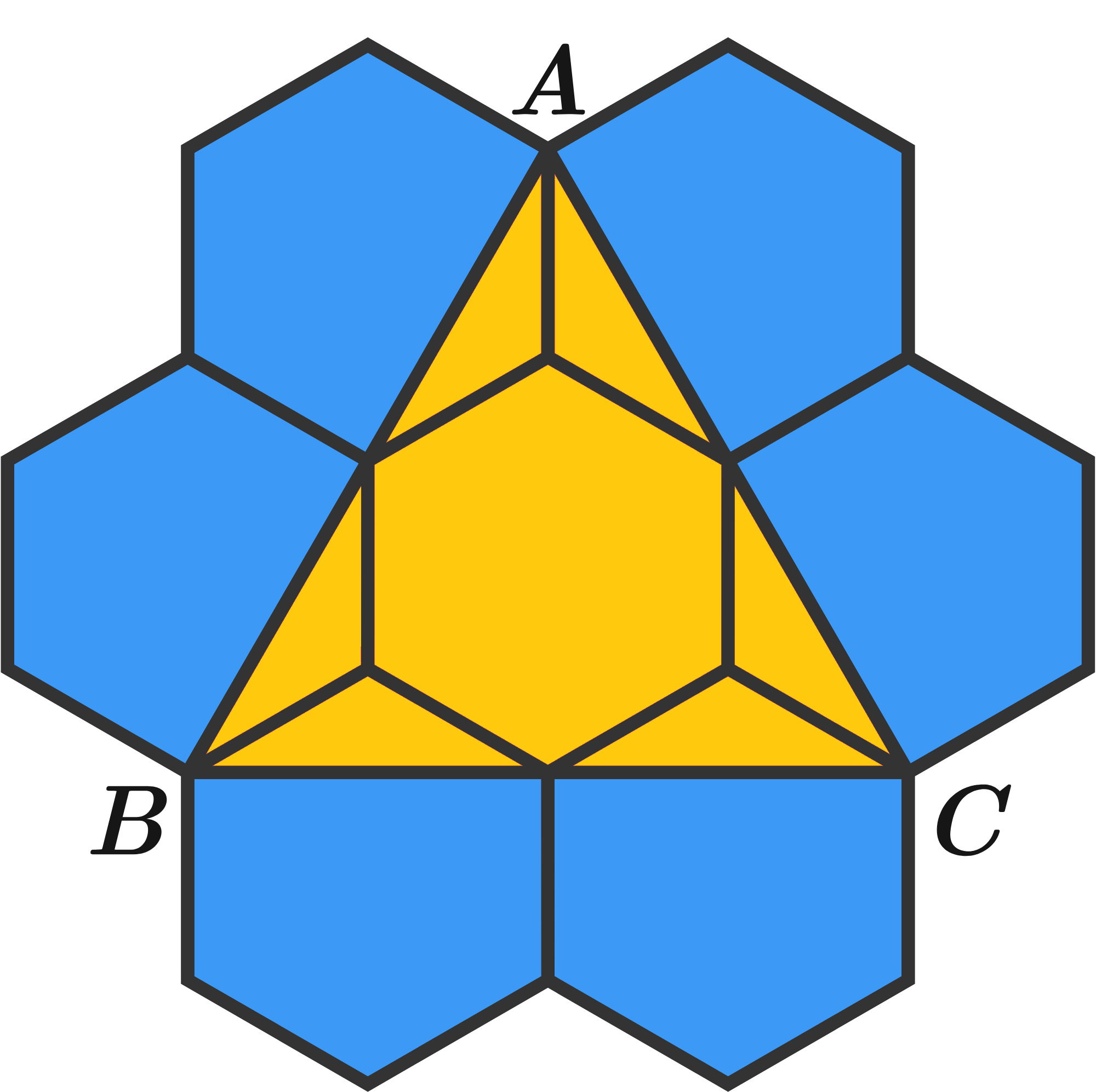
\(7\) identical hexagons are arranged in a pattern on the picture below. Each hexagon has an area of \(8\). What is the area of the triangle \(\triangle ABC\)?
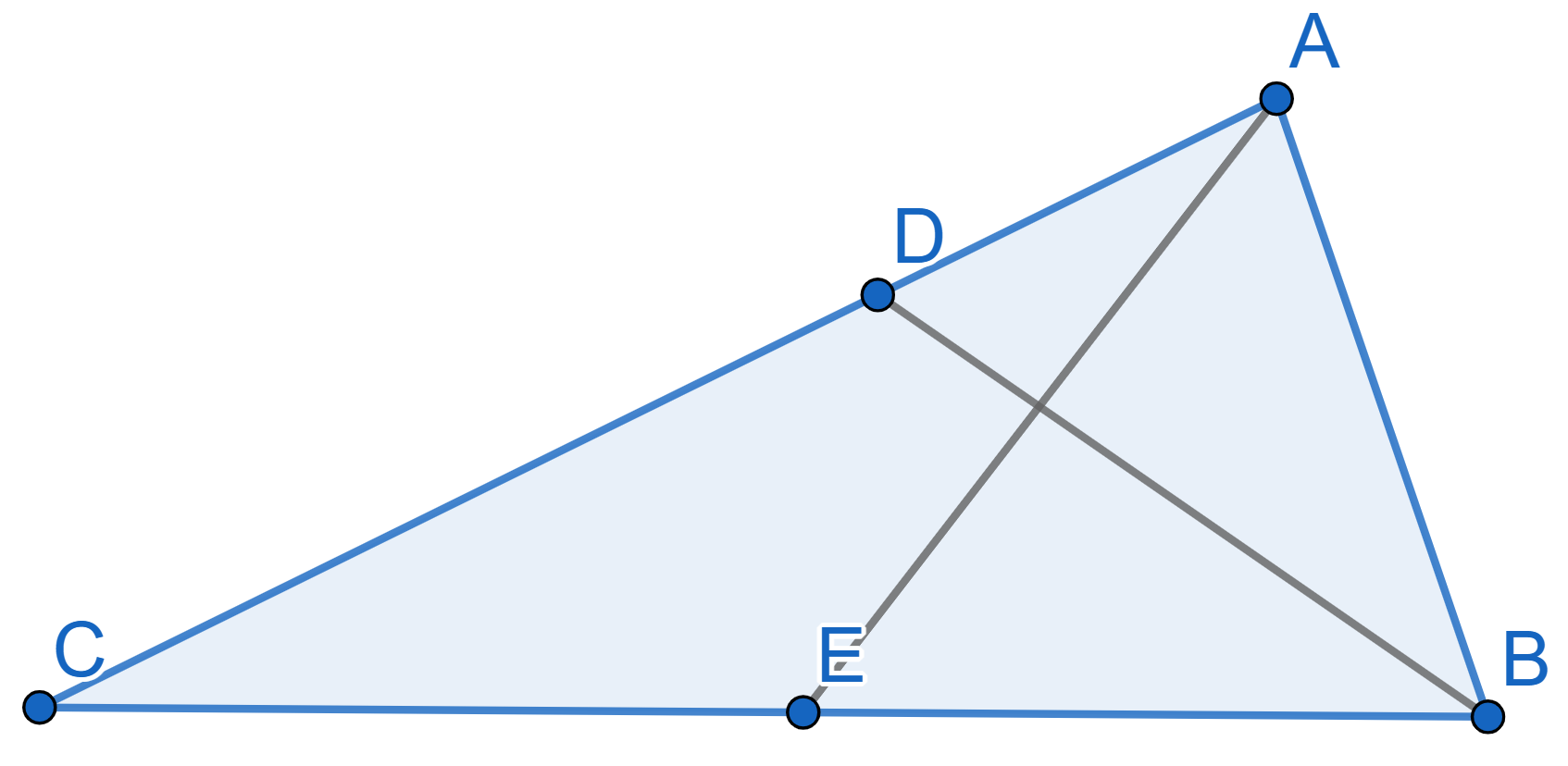
In the triangle \(ABC\) the bisector \(BD\) coincides with the height. Prove that \(AB=BC\).
In the triangle \(ABC\) the median \(BD\) coincides with the height. Prove that \(AB=BC\).
In the triangle \(ABC\) with \(BC=12\), the median \(AE\) is perpendicular to the bisector \(BD\). Find the length of \(AB\).
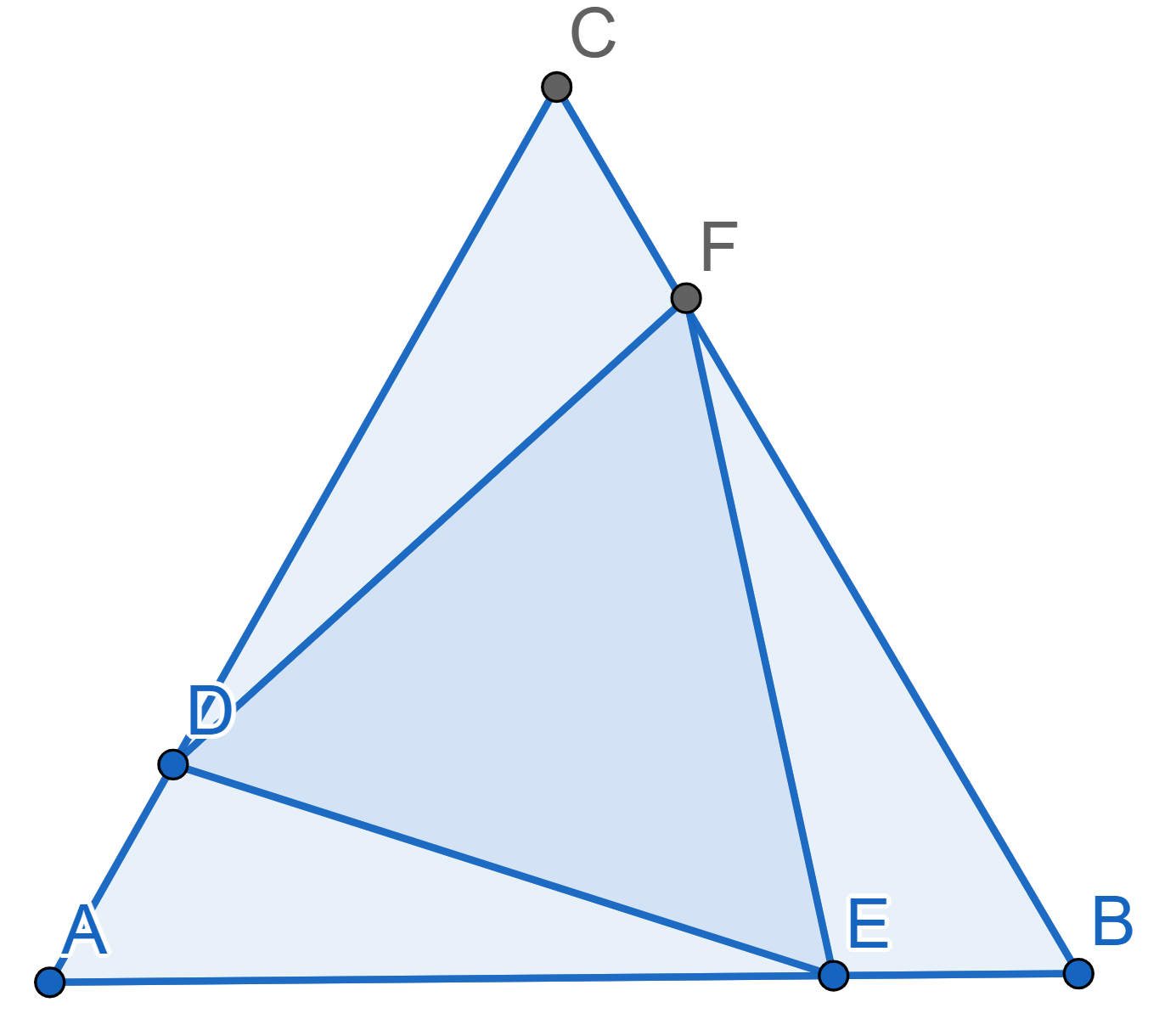
On the sides of the equilateral triangle \(ABC\) three points \(D,E,F\) are chosen in such a way that the
following ratios of lengths hold: \[AD:DC =
CF:FB = BE:AE\] Prove that the triangle \(DEF\) is also equilateral.
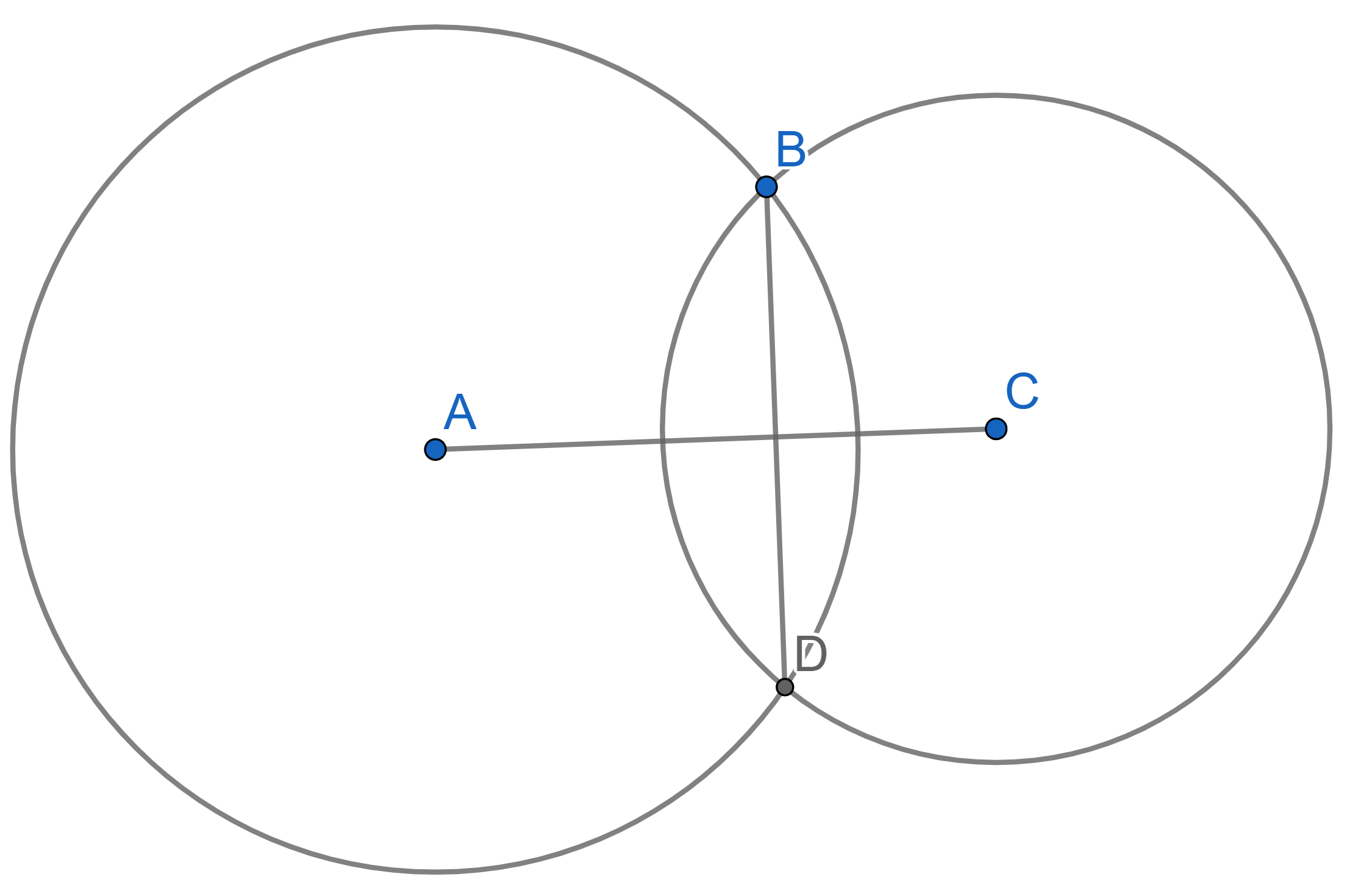
Two circles with centres \(A\) and
\(C\) intersect at the points \(B\) and \(D\). Prove that the segment \(AC\) is perpendicular to \(BD\). Moreover, prove that the segment
\(AC\) divides \(BD\) in half.
For two congruent triangles Prove that their corresponding heights are equal.
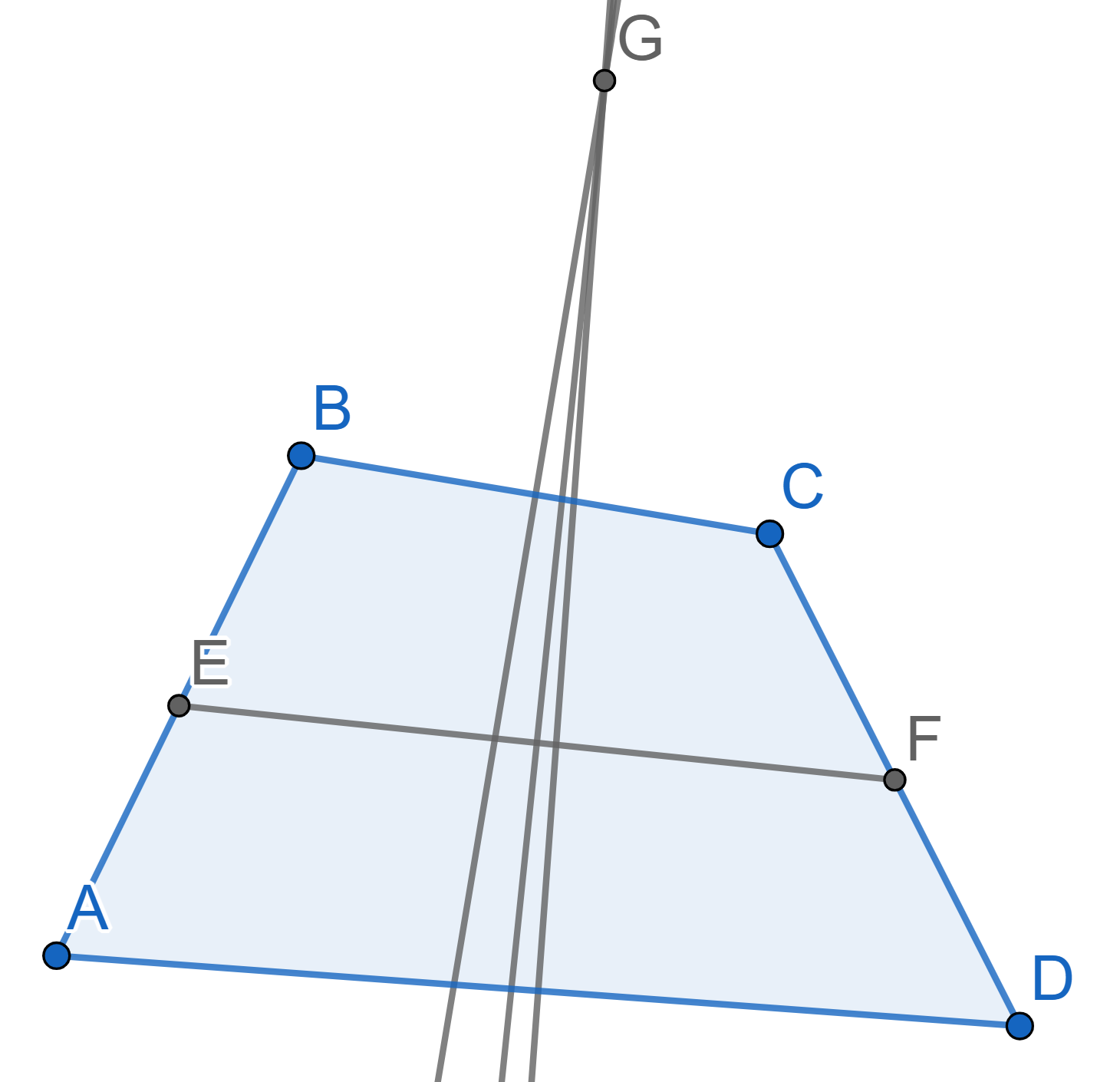
The sides \(AB\) and \(CD\) of the quadrilateral \(ABCD\) are equal, the points \(E\) and \(F\) are the midpoints of \(AB\) and \(CD\) correspondingly. Prove that the
perpendicular bisectors of the segments \(BC\), \(AD\), and \(EF\) intersect at one point.
In the triangle \(ABC\) the heights \(AD\) and \(CE\) intersect at the point \(F\). It is known that \(CF=AF\). Prove that the triangle \(ABC\) is isosceles.
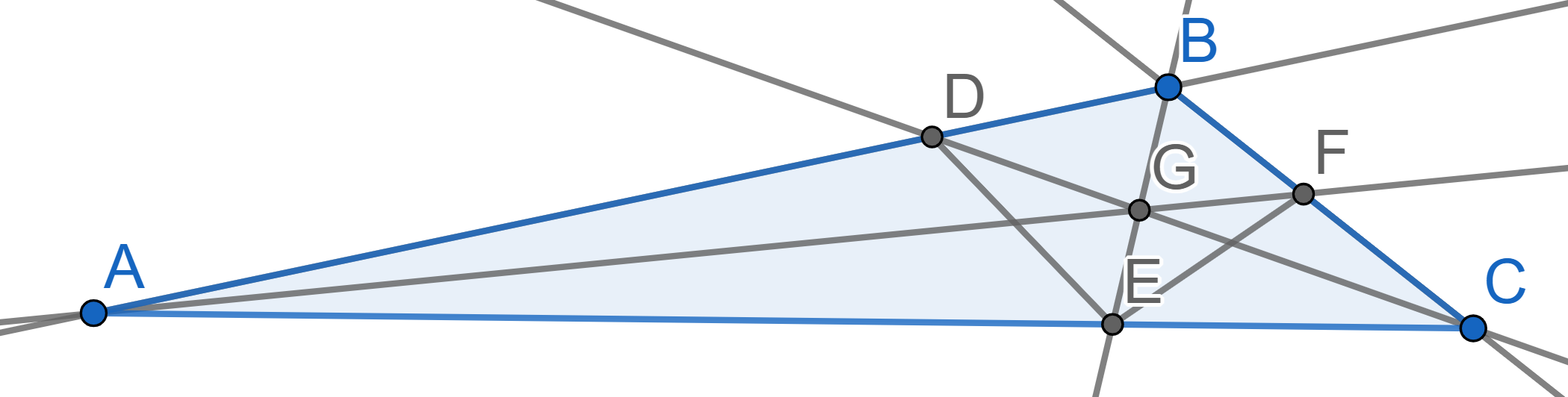
In the triangle \(ABC\) the angle
\(\angle ABC = 120^{\circ}\). The
segments \(AF,\, BE\), and \(CD\) are the bisectors of the corresponding
angles of the triangle \(ABC\). Prove
that the angle \(\angle DEF =
90^{\circ}\).