Problems

How many independent queens can you place on a \(5\times5\) grid? That is, so none of them attack each other.

How many ways can you place \(8\) rooks independently on a chessboard? That is, so that none of them attack each other.

Why are there no closed knight’s tours on an \(n\times n\) grid when \(n\) is odd? A knight’s tour is closed if you can get to the first square from the last square by a knight’s move.

Show how to place fourteen dominating bishops on a standard \(8\times8\) chessboard. That is, every square either contains a bishop, or is attacked by some bishop.

Place eight independent queens on a standard \(8\times8\) chessboard.

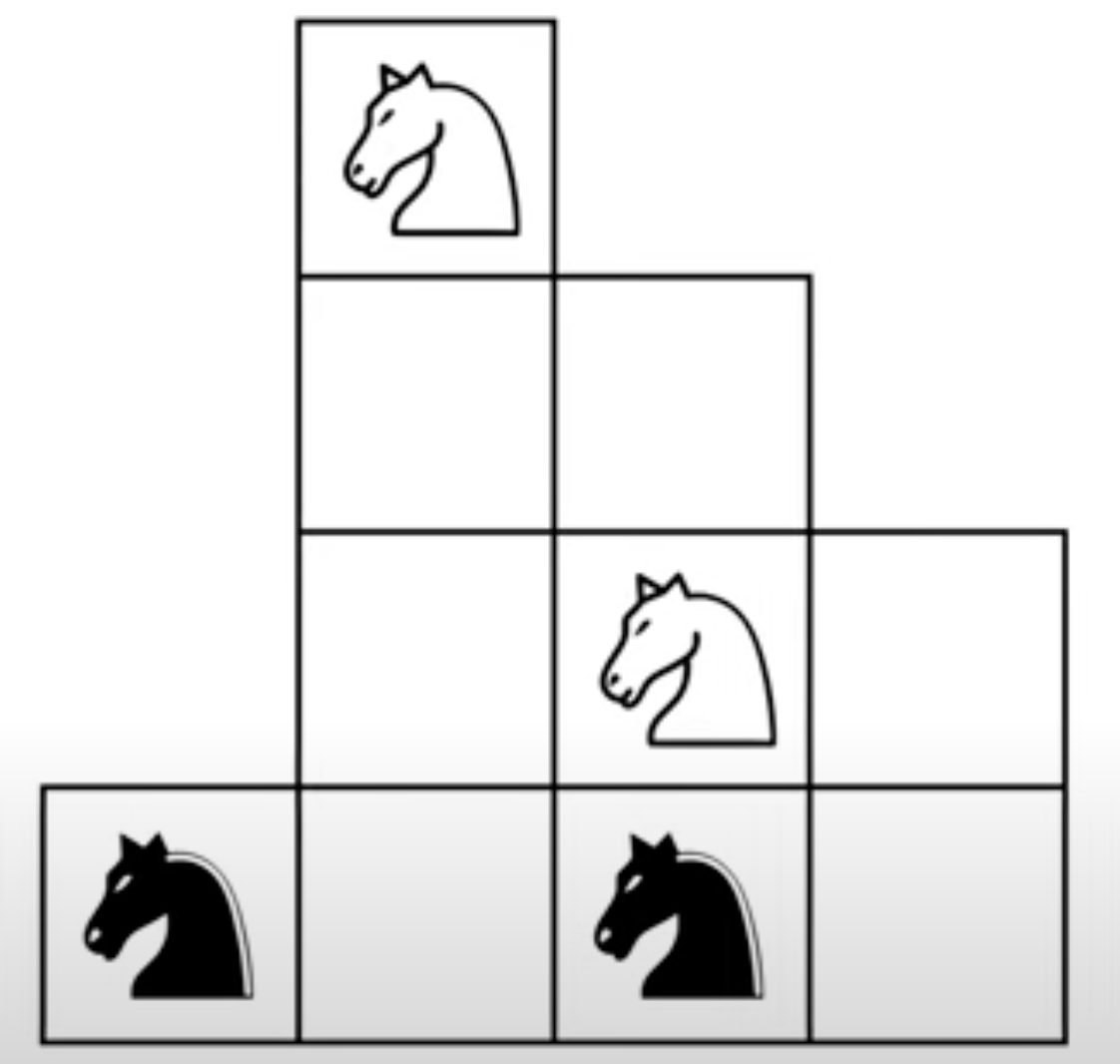
Show how to swap the two pairs of knights on the following strangely-shaped grid. That is, the knights make one move at a time, and you’re trying to get the black nights to where the white knights are, and the white knights to where the black knights are.

Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.

Find an open knight’s tour on a \(2\times2\times2\) cube.

Prove Sperner’s lemma in dimension \(1\), namely on a line.
The simplex in this case is just a segment, the triangulation is subdivision of the segment into multiple small segments, and the conditions of a Sperner’s coloring are the following:

• There are only two colors;

• The opposite ends of the main segment are colored differently;

Then one needs to prove that there exists a small segment with two ends colored in different colors. In particular there is an odd number of such small segments.

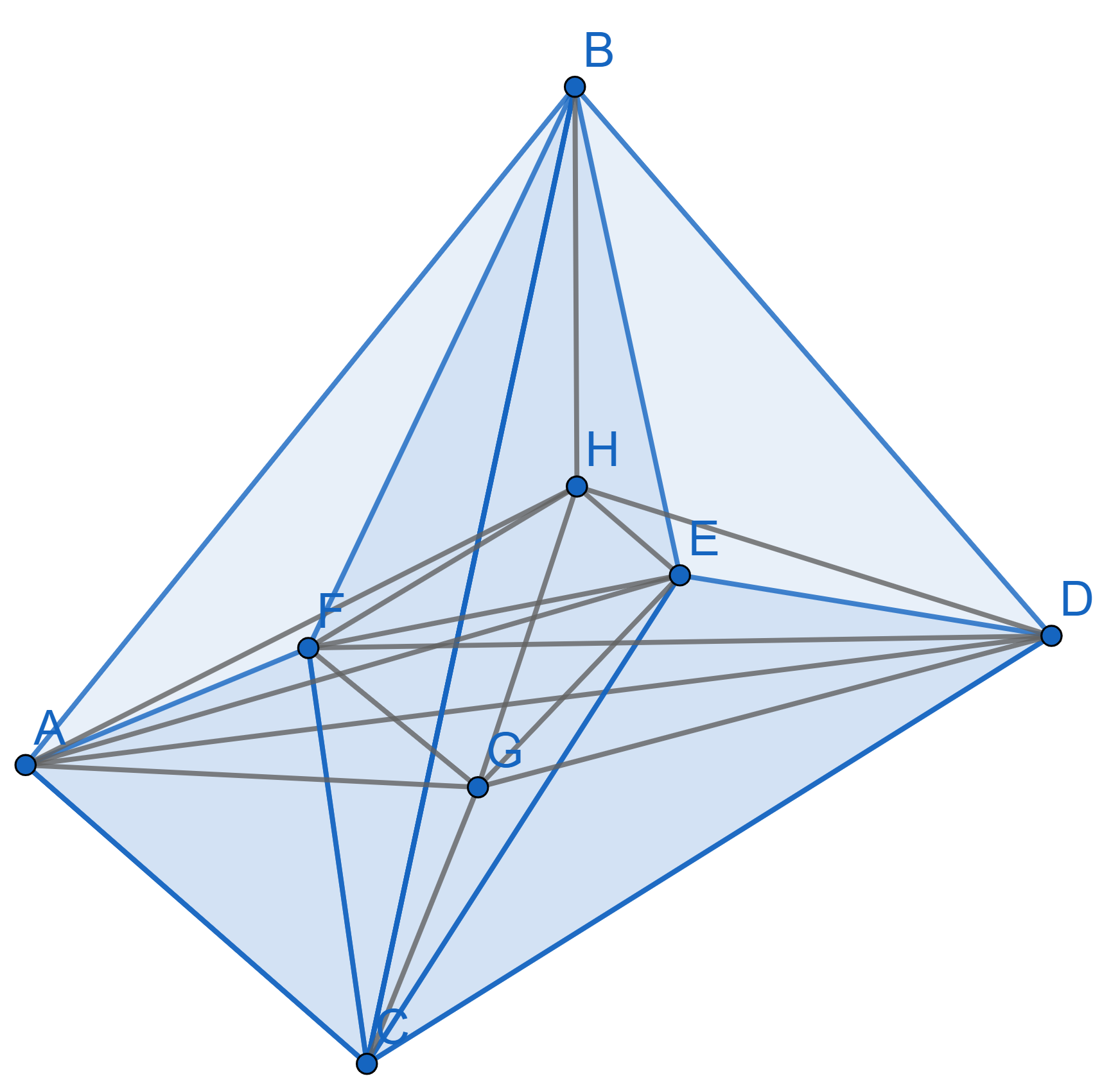
Draw a Sperner’s coloring for the following \(3\)-dimensional simplex. The blue segments are visible, the grey ones are inside the tetrahedron. The point \(F\) is on the face \(ABC\), point \(E\) is on the face \(BCD\), point \(G\) is on the face \(ACD\) and the point \(H\) is on the face \(ABD\).