Problems

The ant crawls a closed path along the edges of the dodecahedron, not turning back anywhere. The path runs exactly twice on each edge. Prove that the ant crawls on some edge of the dodecahedron in the same direction both times.

Given a pile of cards, is it true that reversing the order of the pile by counting the cards out one by one leaves no card in its original position?

How many permutations of $13$ cards swap the third card and the fourth card?

Consider lifting the top $2$ cards from a pile of $6$ cards and placing them at the bottom of the pile. Show how the same process can be done by switching adjacent pairs of cards.

Lennart is a skilled magician - he can shuffle a deck of card in the most arbitrary ways and replicate the shuffle. Once he performed a terribly complicated shuffle and repeated it right away. It turned out all the cards returned to their original position. Show that this complicated shuffle consists of only switching distinct pairs of cards (or keeping some cards where they are).

Take Ace to King of any one suit to make a pile. The cards are in numerical order, so that Ace is at the top and King is at the bottom. Count out four cards from the top one by one and put the rest of the pile on top of the four cards.

If you perform this action a total of $7$ times, what is now the top card?

Here is a half of a magic trick to impress your friends. Take the Ace to Seven of hearts and order them numerically in a pile with Ace at the bottom and Seven at the top. Do the same with the Ace to Seven of spades. Put the pile of spades on top of the pile of hearts. Flip the $14$-card deck so the cards are now face down.

Make a cut anywhere. Deal out $7$ cards from the top into a pile, so that you now have two piles of equal size again. Let us refer to the motion of taking the top card of a pile and putting it to the bottom as making a swap. Making two swaps means doing the motion twice, NOT taking the top two cards at the same time.

Your friend chooses two nonnegative numbers that add up to $6$, for example $4$ and $2$. Make $4$ swaps on the first pile and $2$ swaps on the second pile. Remove the top card of each pile, so that we now have two piles of six cards.

Your friend now chooses two nonnegative numbers that add up to five and repeat the same procedure. We will continue doing this, but at each turn, the total number of swaps decreases by one. Eventually, we should have one card remaining in each pile. It turns out to be a matching pair.

How does the trick work?

Many magicians can perform what is known as the Faro shuffle. Actually there are two kinds of Faro shuffle: the in Faro shuffle and the out Faro shuffle.

Let us assume that the deck has an even number of cards. The first step of the Faro shuffle is to divide the deck into two smaller decks of equal size. One deck consist of the top half of the original deck in their original order. The other deck consists of the bottom half of the original deck in their original order.

The second step of the Faro shuffle is to interweave the two decks, so that each card is above and beneath a card of the opposite deck. This is where the in Faro and the out Faro differ: the in Faro changes the top and bottom cards of the original deck (from before step one) while the out Faro retains the original top and bottom cards.

Show that only 8 out Faro shuffles are needed to return a standard 52 card deck back into its original position.

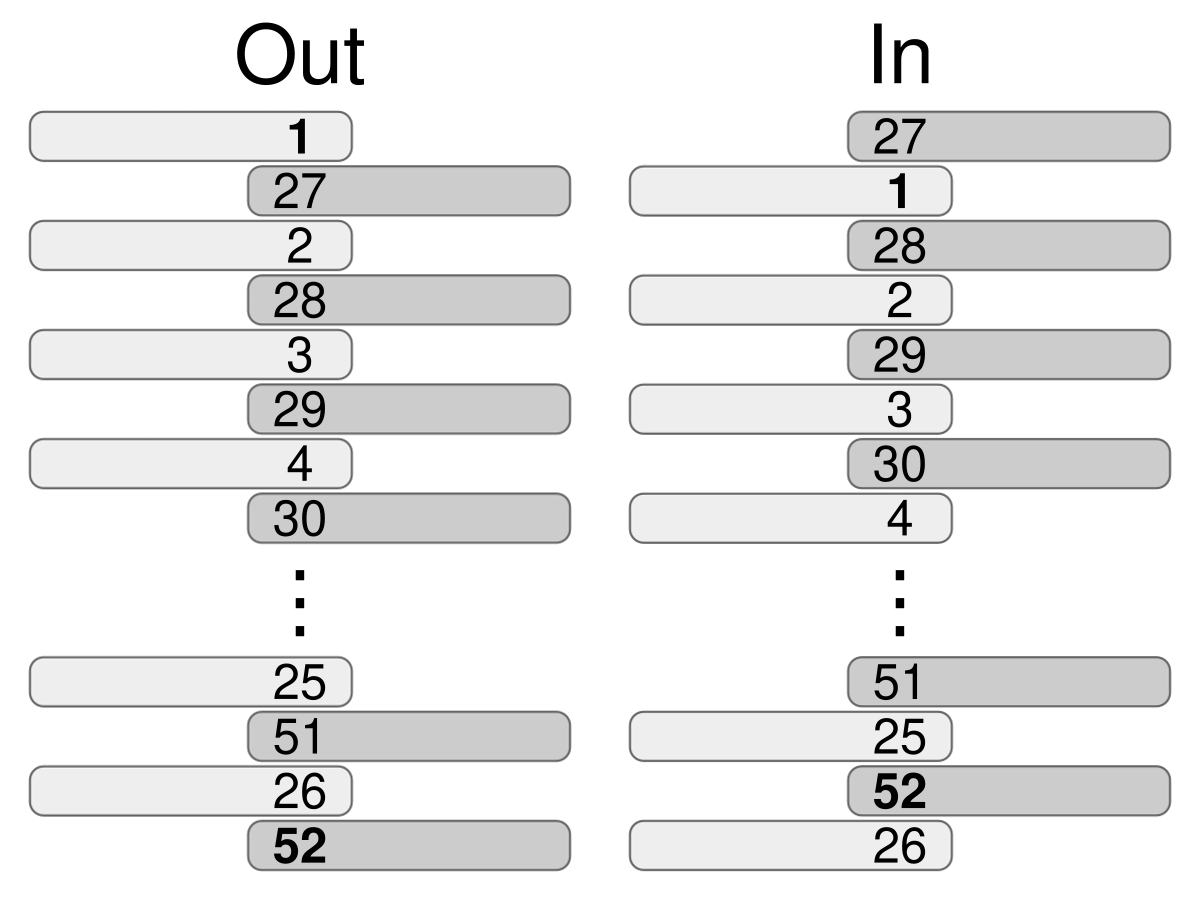
How can you move the top card to any position in an even size deck using only Faro shuffles?

You have a deck of $n$ distinct cards. Deal out $k$ cards from the top one by one and put the rest of the deck on top of the $k$ cards. What is the minimum number of times you need to repeat the action to return every card back to its position?