Problems
A convex polygon on the plane contains at least \(m^2+1\) points with integer coordinates. Prove that it contains \(m+1\) points with integers coordinates that lie on the same line.
Suppose a football team scores at least one goal in each of the \(20\) consecutive games. If it scores a total of \(30\) goals in those \(20\) games, prove that in some sequence of consecutive games it scores exactly \(9\) goals total.
The prime factorization of the number \(b\) is \(2 \times 5^2 \times 7 \times 13^2 \times 17\). The prime factorization of the number \(c\) is \(2^2 \times 5 \times 7^2 \times 13\). Is the first number divisible by the second one? Is the product of these two numbers, \(b \times c\), divisible by \(49000\)?
Determine all prime numbers \(p\) such that \(5p+1\) is also prime.
A graph is called Bipartite if it is possible to split all its vertices into two groups in such a way that there are no edges connecting vertices from the same group. Find out whic of the following graphs are bipartite and which are not:
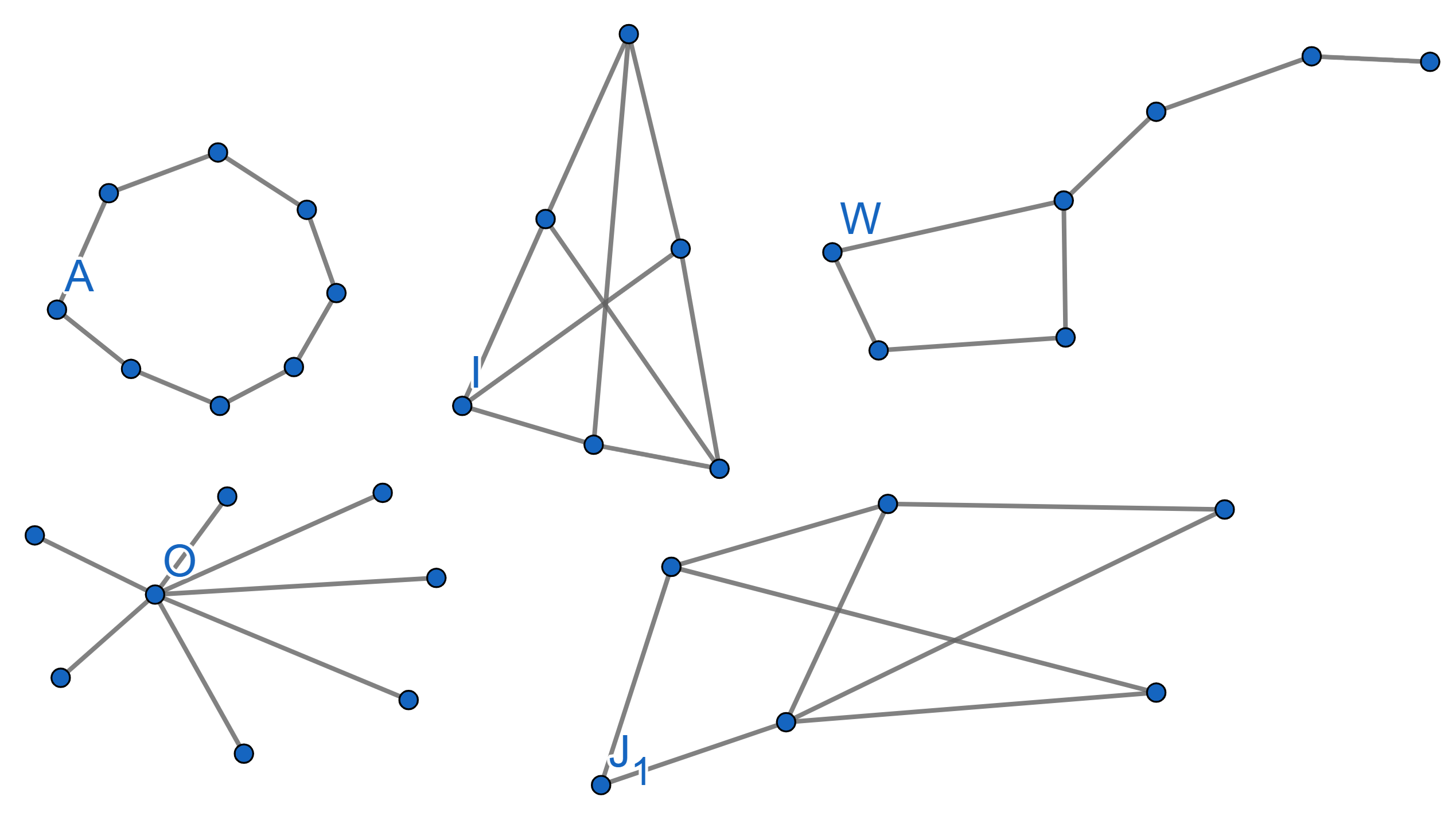
Show that a bipartite graph with \(n\) vertices cannot have more than \(\frac{n^2}{4}\) edges.
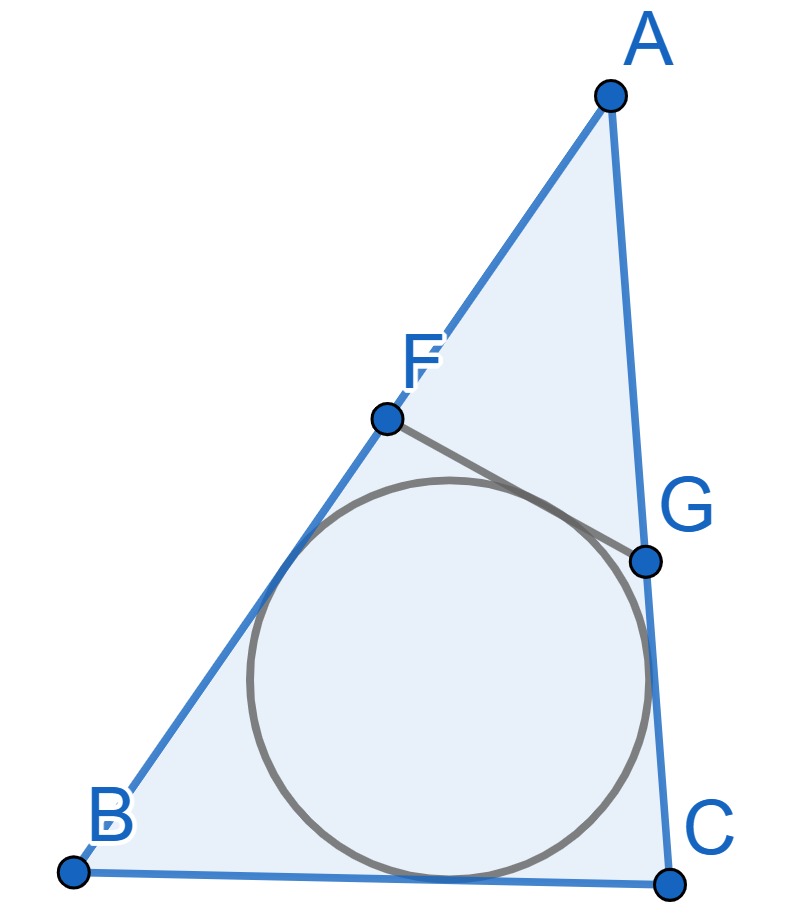
A circle is inscribed into the triangle \(ABC\) with sides \(BC=6, AC=10\) and \(AB= 12\). A line tangent to the circle intersects two longer sides of the triangle \(AB\) and \(AC\) at the points \(F\) and \(G\) respectively. Find the perimeter of the triangle \(AFG\).
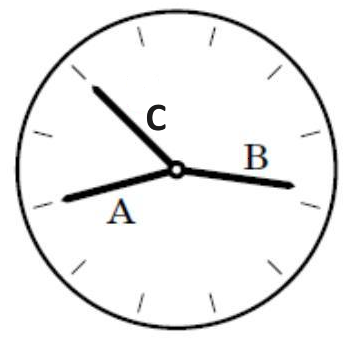
Liam saw an unusual clock in the museum: the clock had no digits, and it’s not clear how the clock should be rotated. That is, we know that \(1\) is the next digit clockwise from \(12\), \(2\) is the next digit clockwise from \(1\), and so on. Moreover all the arrows (hour, minute, and second) have the same length, so it’s not clear which is which. What time does the clock show?
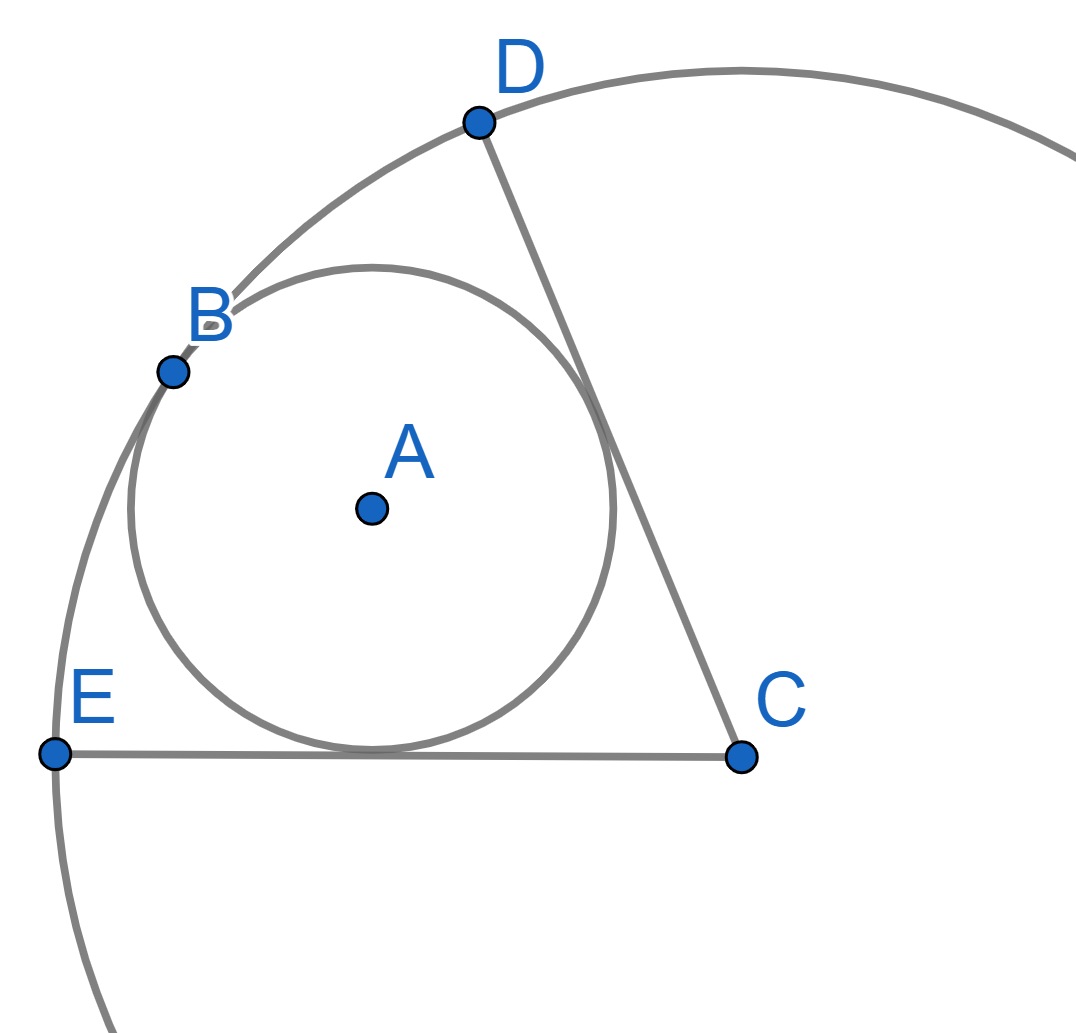
Two circles are tangent to each other and the smaller circle with the center \(A\) is located inside the larger circle with the center \(C\). The radii \(CD\) and \(CE\) are tangent to the smaller circle and the angle \(\angle DCE = 60^{\circ}\). Find the ratio of the radii of the circles.
For positive real numbers \(a,b,c\) prove the inequality: \[(a^2b + b^2c + c^2a)(ab^2 + bc^2 + ca^2)\geq 9a^2b^2c^2.\]