Problems

What is there a greater number of: cats, except for those cats that are not named Fluffy, or animals named Fluffy, except for those that are not cats?

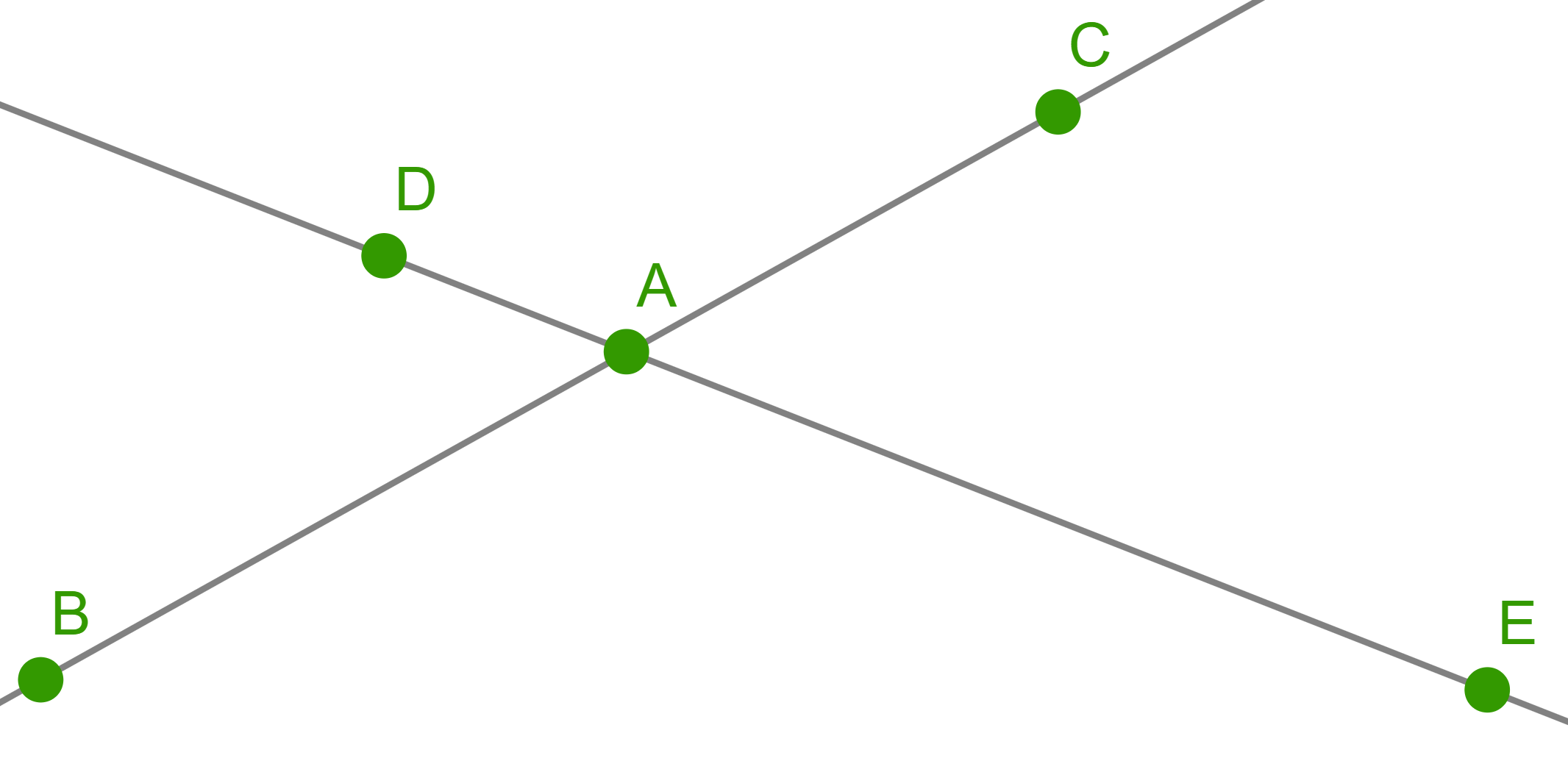
Five oaks are planted along two linear park alleys in such a way that there are three oaks along each alley, see picture. Where should we plant the sixth oak so that it will be possible to lay two more linear alleys, along each of which there would also be three oak trees growing?

Decipher the following puzzle. All the numbers indicated by the letter E, are even (not necessarily equal); all the numbers indicated by the letter O are odd (also not necessarily equal).

The smell of a flowering lavender plant diffuses through a radius of 20 m around it. How many lavender plants must be planted along a straight 400m path so that the smell of the lavender reaches every point on the path.

In a vase, there is a bouquet of 7 white and blue lilac branches. It is known that 1) at least one branch is white, 2) out of any two branches, at least one is blue. How many white branches and how many blue are there in the bouquet?

The angle at the top of a crane is \(20^{\circ}\). How will the magnitude of this angle change when looking at the crane with binoculars which triple the size of everything?

In some country there are 101 cities, and some of them are connected by roads. However, every two cities are connected by exactly one path.

How many roads are there in this country?

Determine all integer solutions of the equation \(yk = x^2 + x\). Where \(k\) is an integer greater than \(1\).

A group of numbers \(A_1, A_2, \dots , A_{100}\) is created by somehow re-arranging the numbers \(1, 2, \dots , 100\).

100 numbers are created as follows: \[B_1=A_1,\ B_2=A_1+A_2,\ B_3=A_1+A_2+A_3,\ \dots ,\ B_{100} = A_1+A_2+A_3\dots +A_{100}.\]

Prove that there will always be at least 11 different remainders when dividing the numbers \(B_1, B_2, \dots , B_{100}\) by 100.

There are 68 coins, and it is known that any two coins differ in weight. With 100 weighings on a two-scales balance without weights, find the heaviest and lightest coin.