Problems
How do you cut a rectangular cake into two equal pieces when someone has already removed a rectangular piece from it? The removed piece can be of any size or orientation. You are allowed just one straight cut.
You have 26 constants, labeled \(A\) through \(Z\). Let \(A\) equal 1. The other constants have values equal to the letter’s position in the alphabet, raised to the power of the previous constant. That means that \(B\) (the second letter) = \(2^A=2^1= 2\), \(C = 3^B=3^2= 9\), and so on. Find the exact numerical value for this expression: \[(X-A)(X-B)(X-C)\dots (X-Y)(X-Z).\]
Why does a mirror reverse right and left instead of up and down?
After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:
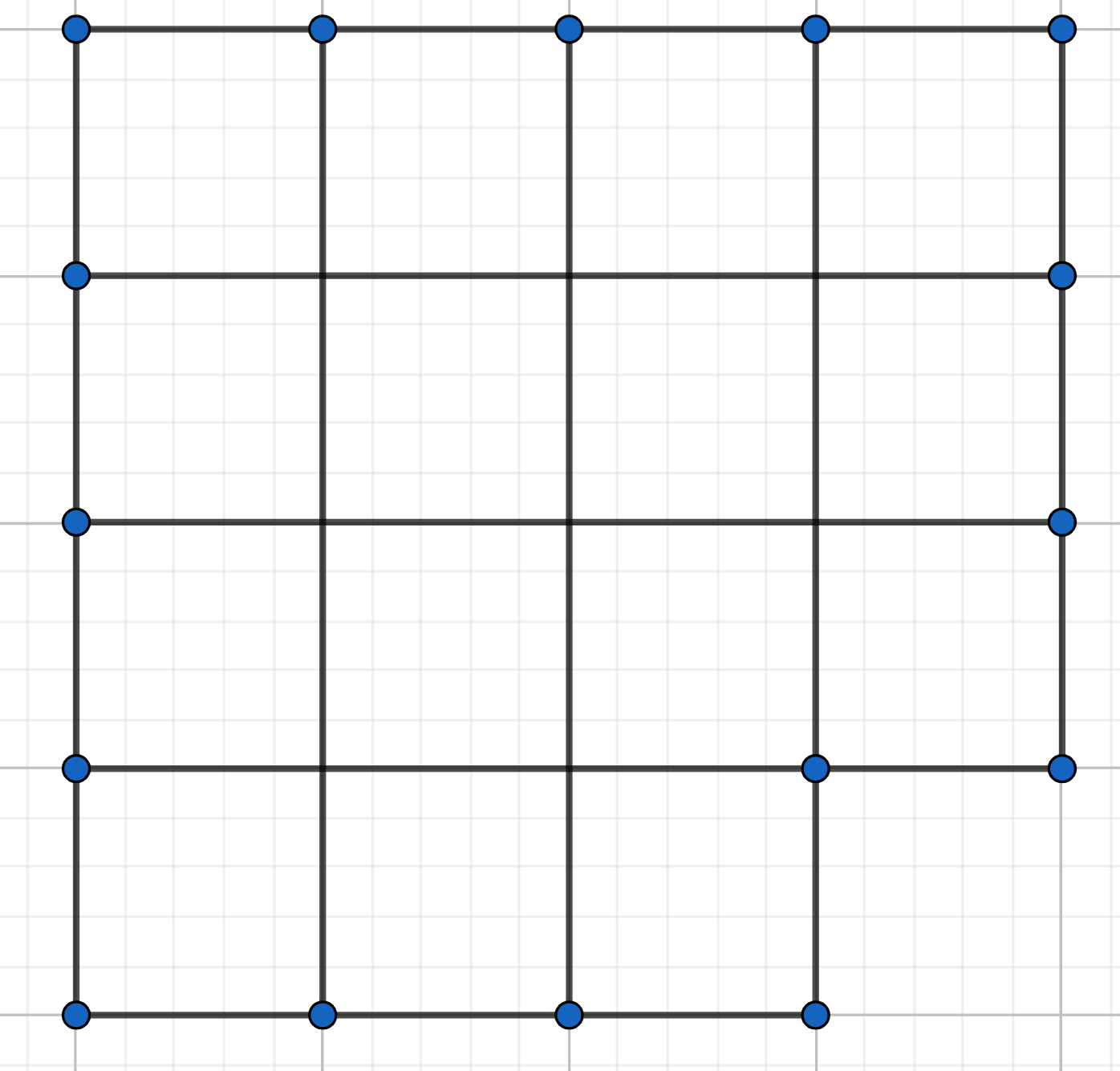
how can we cut this into three congruent shapes?
Max asked Emily how old she was. She replied that she was 13 years old the day before yesterday, and will be 16 next year. Then, Max asked her brother, whether it was true, and he said yes. How is it possible if nobody was lying?
Ten little circles are drawn on the following \(4\times 4\) board:
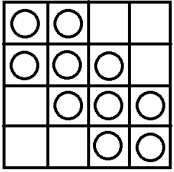
Is it possible to cut the board into four identical parts, in such a way that each part contains 1, 2, 3, and 4 circles correspondingly?
The date 21.02.2012 reads the same forwards and backwords (such numbers are called palindromes). Are there any more palindrome dates in the twenty first centuary?
Do there exist three natural numbers such that neither of them divide each other, but each number divides the product of the other two?
Find all the solutions of the puzzle and prove there are no others. Different letters denote different digits, while the same letters correspond to the same digits. \[M+MEEE=BOOO.\]
Philip and Denis cut a watermelon into four parts. When they finished eating watermelon (they ate the whole thing), they discovered that there were five watermelon rinds left. How is it possible, if no rind was cut after the initial cutting?