Problems

Given a pile of five cards, is it true that reversing the order of the pile by counting the cards out one by one leaves no card in its original position?

Today we will discover some ideas related to non-isosceles triangles. This restriction comes from the fact that in isosceles triangles, a median and a height coincide.

Let \(p\) be a prime number, \(a\) be an integer, not divisible by \(p\). Prove that \(a^p-a\) is divisible by \(p\).

Let \(n\) be an integer. Denote by \(\phi(n)\) the number of integers from \(1\) to \(n-1\) coprime to \(n\). Find \(\phi(n)\) in the following cases:

• \(n\) is a prime number.

• \(n = p^k\) for a prime \(p\).

• \(n=pq\) for two different primes \(p\) and \(q\).

Let \(n\) be an integer and let \(a\) be an integer coprime to \(n\). Prove that \(a^{\phi(n)-1}-1\) is divisible by \(n\).

With a pile of four cards, does reversing the order of the pile by counting the cards out one by one leaves no card in its original position?

You have in your hands a royal flush! That is, Ace, King, Queen, Jack and \(10\) of spades. How many shuffles of your hand swap the Ace and Jack?

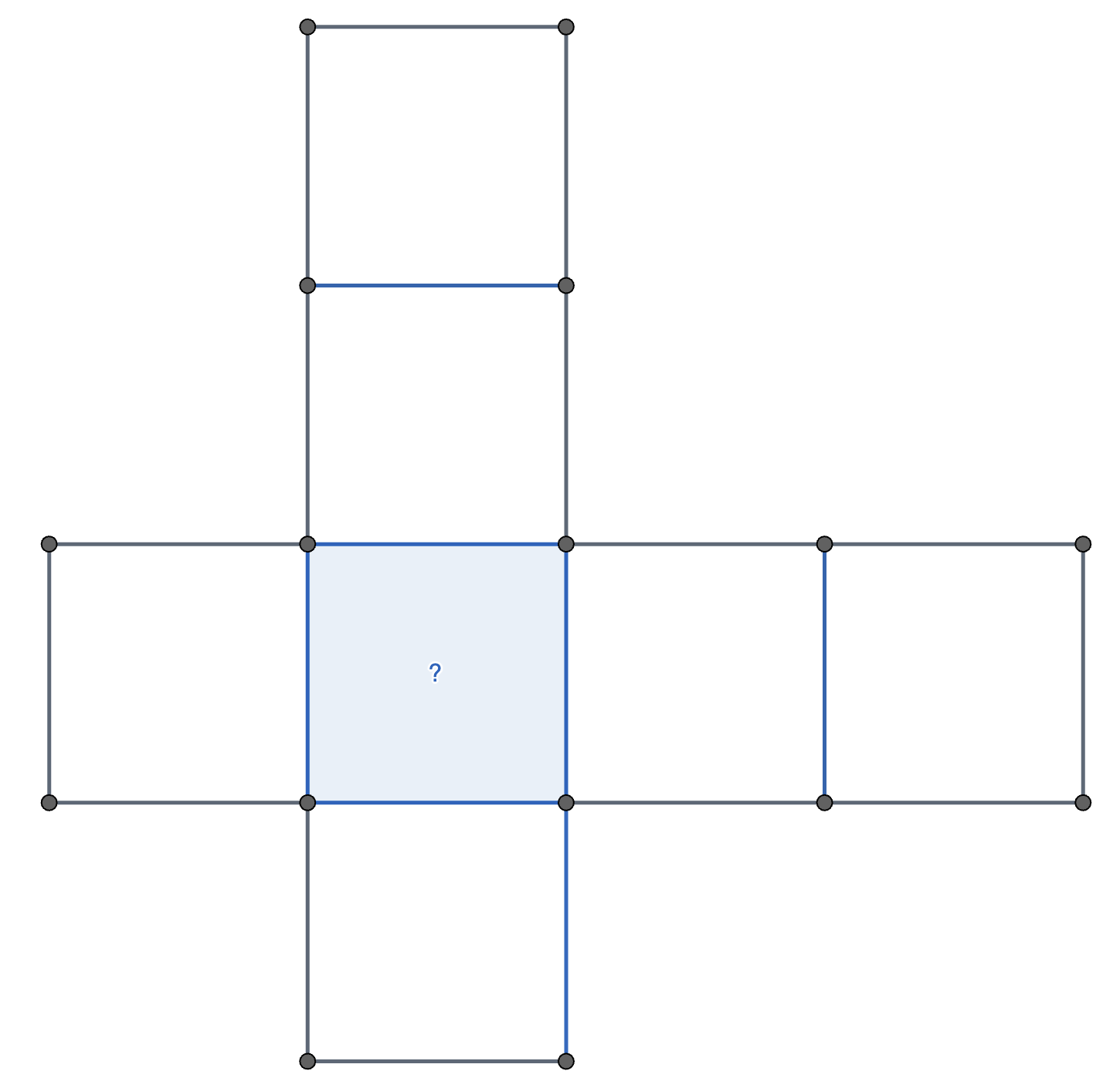
In the diagram below, I wish to write the numbers \(6, 11, 19, 23, 25, 27\) and \(29\) in the squares, but I want the sum of the numbers in the horizontal row to equal the sum of the numbers in the vertical column. What number should I put in the blue square with the question mark?

You have a row of coins and you can perform these three operations as many times as you like:

1. Remove three adjacent heads

2. Remove two adjacent tails

3. If there’s a tail followed by a heads, then turn the tail over and put a new tail after both heads

You apply these operations until you can’t make any more moves. Show that you will always get the same configuration at the end, no matter the order.

Let \(a\) be a positive integer, and let \(p\) be a prime number. Prove that \(a^p - a\) is a multiple of \(p\).