A student did not notice the multiplication sign between two three-digit numbers and wrote one six-digit number. The result was three times greater.
Find these numbers.
There is a chocolate bar with five longitudinal and eight transverse grooves, along which it can be broken (in total into \(9 * 6 = 54\) squares). Two players take part, in turns. A player in his turn breaks off the chocolate bar a strip of width 1 and eats it. Another player who plays in his turn does the same with the part that is left, etc. The one who breaks a strip of width 2 into two strips of width 1 eats one of them, and the other is eaten by his partner. Prove that the first player can act in such a way that he will get at least 6 more chocolate squares than the second player.
A village infant school has 20 pupils. If we pick any two pupils they will have a shared granddad.
Prove that one of the granddads has no fewer than 14 grandchildren who are pupils at this school.
During the ball every young man danced the waltz with a girl, who was either more beautiful than the one he danced with during the previous dance, or more intelligent, but most of the men (at least 80%) – with a girl who was at the same time more beautiful and more intelligent. Could this happen? (There was an equal number of boys and girls at the ball.)
A \(1 \times 10\) strip is divided into unit squares. The numbers \(1, 2, \dots , 10\) are written into squares. First, the number 1 is written in one square, then the number 2 is written into one of the neighboring squares, then the number 3 is written into one of the neighboring squares of those already occupied, and so on (the choice of the first square is made arbitrarily and the choice of the neighbor at each step). In how many ways can this be done?
4 points \(a, b, c, d\) lie on the segment \([0, 1]\) of the number line. Prove that there will be a point \(x\), lying in the segment \([0, 1]\), that satisfies \[\frac{1}{ | x-a |}+\frac{1}{ | x-b |}+\frac{1}{ | x-c |}+\frac{1}{ | x-d |} < 40.\]
On a plane there is a square, and invisible ink is dotted at a point \(P\). A person with special glasses can see the spot. If we draw a straight line, then the person will answer the question of on which side of the line does \(P\) lie (if \(P\) lies on the line, then he says that \(P\) lies on the line).
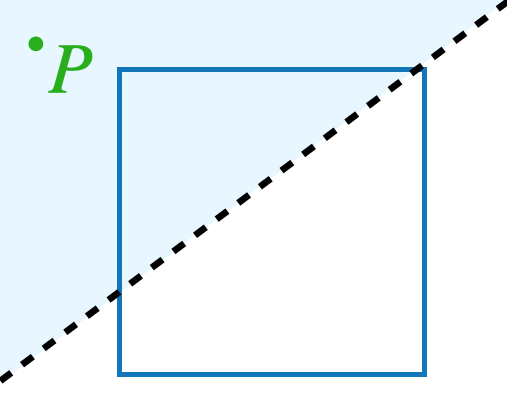
What is the smallest number of such questions you need to ask to find out if the point \(P\) is inside the square?
Let \(n\) numbers are given together with their product \(p\). The difference between \(p\) and each of these numbers is an odd number.
Prove that all \(n\) numbers are irrational.
Two play tic-tac-toe on a \(10 \times 10\) board according to the following rules. First they fill the whole board with noughts and crosses, putting them in turn (the first player puts crosses, their partner – noughts). Then two numbers are counted: \(K\) is the number of five consecutively standing crosses and \(H\) is the number of five consecutively standing zeros. (Five, standing horizontally, vertically and parallel to the diagonal are counted, if there are six crosses in a row, this gives two fives, if there are seven, then three, etc.). The number \(K-H\) is considered to be the winnings of the first player (the losses of the second).
a) Does the first player have a winning strategy?
b) Does the first player have a non-losing strategy?
Some real numbers \(a_1, a_2, a_3,\dots ,a _{2022}\) are written in a row. Prove that it is possible to pick one or several adjacent numbers, so that their sum is less than 0.001 away from a whole number.